题目内容
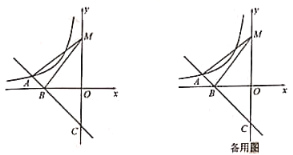
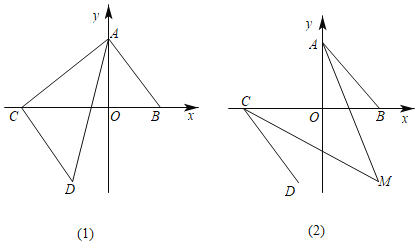
【题目】如图,在平面直角坐标系中,已知点A(0,4),B(3,0),线段AB平移后对应的线段为CD,点C在x轴的负半轴上,B、C两点之间的距离为8.
(1)求点D的坐标;
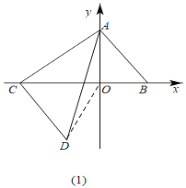
(2)如图(1),求△ACD的面积;
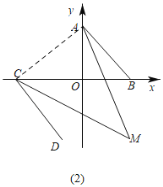
(3)如图(2),∠OAB与∠OCD的角平分线相交于点M,探求∠AMC的度数并证明你的结论.
【答案】(1)D(﹣2,﹣4);(2)16;(3)∠M=45°,理由见解析
【解析】
(1)根据平移规律可得点D的坐标;
(2)利用面积差可得结论;
(3)先根据直角三角形的两锐角互余得:∠OAB+∠ABO=90°,由角平分线定义得:∠MCB+∠OAM=![]() (∠DCB+∠OAB)=45°,最后根据三角形的内角和可得结论.
(∠DCB+∠OAB)=45°,最后根据三角形的内角和可得结论.
解:(1)∵ B(3,0),
∴ OB=3,
∵ BC=8,
∴ OC=5,
∴ C(﹣5,0),
∵ AB∥CD,AB=CD,
∴ D(﹣2,﹣4);
(2)如图(1),连接OD,
∴S△ACD=S△ACO+S△DCO﹣S△AOD=![]() ﹣
﹣![]() =16;
=16;
(3)∠M=45°,理由是:
如图(2),连接AC,
∵AB∥CD,
∴∠DCB=∠ABO,
∵∠AOB=90°,
∴∠OAB+∠ABO=90°,
∴∠OAB+∠DCB=90°,
∵∠OAB与∠OCD的角平分线相交于点M,
∴∠MCB=![]() ,∠OAM=
,∠OAM=![]() ,
,
∴∠MCB+∠OAM=![]() =45°,
=45°,
△ACO中,∠AOC=∠ACO+∠OAC=90°,
△ACM中,∠M+∠ACM+∠CAM=180°,
∴∠M+∠MCB+∠ACO+∠OAC+∠OAM=180°,
∴∠M=180°﹣90°﹣45°=45°.

练习册系列答案
相关题目