题目内容
【题目】如图,在平行四边形ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
(1)求证:EG//FH;
(2)GH、EF互相平分.

【答案】(1)见解析 (2)见解析
【解析】
(1)由平行四边形的性质得到AB平行CD,得到内错角∠GAO=∠FCH,根据AF=CE,同时减去EF可得AE=CF,根据SAS可证△ AGE≌△CHF,得到∠AEG=∠CFH,再由邻补角得到内错角相等,得到两线平行;
(2)连接FG、EH ,由(1)可证四边形EGFH是平行四边形即可得到结论.
在ABCD中,
∵AB∥CD,
∴∠GAE=∠HCF,
∵AF=CE,
∴AF-EF=CE=EF,
即;AE=CF,
在△AGE与△CHF中,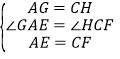 ,
,
∴△AGE≌△CHF(SAS),
∴∠AEG=∠CFH,
∴∠GEO=∠HFO,
∴EG∥FH;
(2)连接FG、EH
由(1)证得△AGE≌△CHF ,EG∥FH,
∴GE=HF,
∴四边形GFHE是平行四边形,
∴GH、EF互相平分.


练习册系列答案
相关题目