题目内容
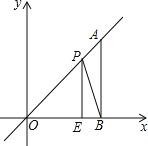
【题目】林城市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
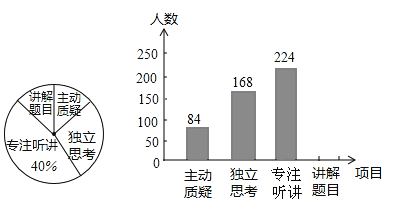
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
【答案】(1)560(2)见解析(3)4.8万人
【解析】
解:(1)560。
(2)讲解题目的学生数为:560﹣84﹣168﹣224=560﹣476=84,补全统计图如图;

(3)![]() ×16=4.8(万人),
×16=4.8(万人),
答:在试卷讲评课中,“独立思考”的学生约有4.8万人。
(1)根据扇形统计图专注听讲的百分比与条形统计图中专注听讲的人数,列式计算即可:224÷40%=560名。
(2)用被抽查的学生人数减去主动质疑、独立思考、专注听讲的人数,求出讲解题目的人数,然后补全统计图即可。
(3)用独立思考的学生的百分比乘以16万,进行计算即可得解。

练习册系列答案
相关题目
【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图象与性质,探究过程如下,请补充完整.
的图象与性质,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ,
,![]() ;
;
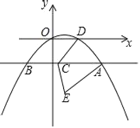
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
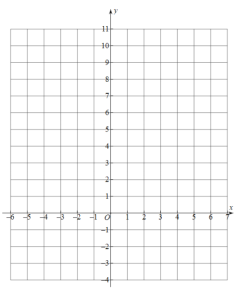
(3)观察函数图象:
①当方程![]() 有且仅有两个不相等的实数根,根据函数图象直接写出
有且仅有两个不相等的实数根,根据函数图象直接写出![]() 的取值范围为 ;
的取值范围为 ;
②在该平面直角坐标系中画出直线![]() 的图象,根据图象直接写出该直线与函数
的图象,根据图象直接写出该直线与函数![]()
![]() 的交点横坐标为: (结果保留一位小数).
的交点横坐标为: (结果保留一位小数).