题目内容
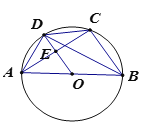
【题目】如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙D于点D,交AC于点E,连接AD,BD,CD若AB=10,cos∠ABC=![]() ,则tan∠DBC的值是( )
,则tan∠DBC的值是( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
【答案】A
【解析】
由AB=10,cos∠ABC=![]() ,可求得OE的长,继而求得DE,AE的长,则可求得tan∠DAE,然后由圆周角定理得∠DBC=∠DAE,则可求得答案.
,可求得OE的长,继而求得DE,AE的长,则可求得tan∠DAE,然后由圆周角定理得∠DBC=∠DAE,则可求得答案.
解:∵AB为直径,AB=10,
∴∠ACB=90°,OA=OD=![]() AB=5,
AB=5,
∵OD∥BC,
∴∠AEO=∠ACB=90°,∠AOE=∠ABC,
在Rt△AEO中,OE=OAcos∠AOE=OAcos∠ABC=5×![]() =3,
=3,
∴DE=ODOE=53=2,
∴AE=![]() ,
,
在Rt△AED中,tan∠DAE=![]() ,
,
∵∠DBC=∠DAE,
∴tan∠DBC=![]() .
.
故选:A.

练习册系列答案
相关题目