题目内容
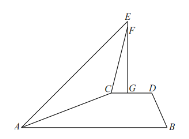
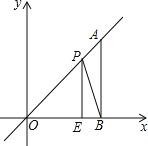
【题目】如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
A.4+2![]() B.4+
B.4+![]() C.6D.4
C.6D.4![]()
【答案】C
【解析】
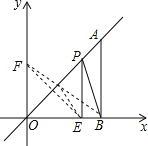
在y轴的正半轴上截取OF=OE=3,连接EF,根据题意连接BF交OA于P,可知此时△BEP周长最小,最小值为BF+EB,再根据勾股定理即可求解.
在y轴的正半轴上截取OF=OE=3,连接EF,
∵A点为直线y=x上一点,
∴OA垂直平分EF,
∴E、F是直线y=x的对称点,
连接BF交OA于P,根据两点之间线段最短可知此时△BEP周长最小,最小值为BF+EB;
∵OF=3,OB=4,
∴BF=![]() =5,
=5,
∵EB=4﹣3=1,
△BEP周长最小值为BF+EB=5+1=6.
故选:C.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目