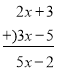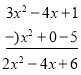题目内容
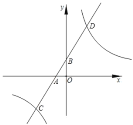
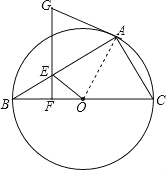
【题目】如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)判断AG与⊙O的位置关系,并说明理由.
(2)若BA=8,∠B=37°,求直径BC的长(结果精确到0.01).

【答案】(1)AG与⊙O相切,理由见解析;(2)10.02.
【解析】
试题(1)利用等腰三角形的性质结合三角形内角和定理得出∠BAO+∠GAE=90°,进而得出答案;
(2)利用锐角三角函数关系得出BC=![]() 即可得出答案.
即可得出答案.
试题解析:(1)AG与⊙O相切,
证明:如图 连接OA,
∵OA=OB,GA=GE,
∴∠ABO=∠BAO,∠GEA=∠GAE.
∵EF⊥BC,
∴∠BFE=90°.
∴∠ABO+∠BEF=90°.
又∵∠BEF=∠GEA,
∴∠GAE=∠BEF.
∴∠BAO+∠GAE=90°.
∴OA⊥AG,即AG与⊙O相切.
(2)∵BC为直径,
∴∠BAC=90°,
在Rt△BAC中,∠BAC=90°.
∵BA=8,∠B=37°,
∴BC=![]() ≈10.02.
≈10.02.

练习册系列答案
相关题目