Question

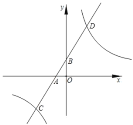
【题目】如图，过抛物线y＝ax2+bx上一点A（4，﹣2）作x轴的平行线，交抛物线于另一点B，点C在直线AB上，抛物线交x轴正半轴于点D（2，0），点B与点E关于直线CD对称．

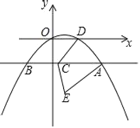
（1）求抛物线的表达式；

（2）①若点E落在抛物线的对称轴上，且在x轴下方时，求点C的坐标．②AE最小值为　 　．

Answer 1

【答案】（1）y＝﹣x2+x；（2）①C的坐标为（，﹣2），②AE的最小值为2﹣2，见解析.

【解析】

（1）将点A（4，-2）、D（2，0）代入求出a、b的值即可得；
（2）①连接BD、DE，作EP⊥AB，并延长交OD于Q，先求出B（-2，-2）、BD=2，设C（m，-2），知BC=CE=m+2，DE=BD=2，由QD=1，PQ=2知PE=QE-PQ=，由PC=1-m及PC2+PE2=CE2可得m的值，从而得出答案；

②由DB=DE=2，知点E在以D为圆心、2长为半径的⊙D上，连接DA，并延长交⊙D于点E′，此时AE′取得最小值，根据AE的最小值为DE-DA可得答案．

解：（1）将点A（4，﹣2）、D（2，0）代入，

得：，

解得：，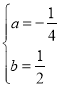

∴抛物线的表达式为y＝﹣x2+x；

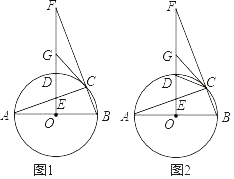
（2）①如图1，连接BD、DE，作EP⊥AB，并延长交OD于Q，

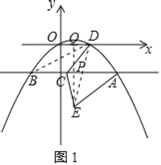
∵抛物线的对称轴为直线x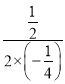＝﹣＝1，

∴点A（4，﹣2）关于对称轴对称的点B坐标为（﹣2，﹣2），

∴BD＝＝2，

设C（m，﹣2），

则BC＝CE＝m+2，DE＝BD＝2，

∵QD＝1，PQ＝2，

∴PE＝QE﹣PQ＝﹣1＝﹣1，

∵PC＝1﹣m，

∴由PC2+PE2＝CE2可得（1﹣m）2+（﹣1）2＝（m+2）2，

解得m＝，

∴点C的坐标为（，﹣2）；

②如图2，

∵DB＝DE＝2，

∴点E在以D为圆心、2长为半径的⊙D上，

连接DA，并延长交⊙D于点E′，此时AE′取得最小值，

∵DA＝＝2，

则AE的最小值为DE﹣DA＝2﹣2，

故答案为：2﹣2．