Question

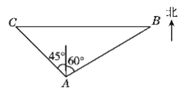
【题目】如图，一艘轮船在小岛的北偏东方向距小岛的处，沿正西方向航行后到达小岛的北偏西方向的处，则该船行驶的速度为______.

Answer 1

【答案】

【解析】

设该船行驶的速度为x海里/时，由已知可得BC=3x，AQ⊥BC，∠BAQ=60°，∠CAQ=45°，AB=80海里，在直角三角形ABQ中求出AQ、BQ，再在直角三角形AQC中求出CQ，得出BC=，解方程即可．

解：如图所示：

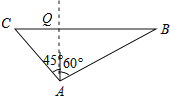
设该船行驶的速度为x海里/时，3小时后到达小岛的北偏西45°的C处，

由题意得：AB=80海里，BC=3x海里，

在直角三角形ABQ中，∠BAQ=60°，

∴∠B=90°-60°=30°，

∴AQ=AB=40，BQ=AQ=40，

在直角三角形AQC中，∠CAQ=45°，

∴CQ=AQ=40，

∴BC=40+40=3x，

解得：．

故答案为：.