题目内容
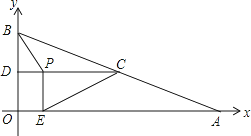
【题目】如图1,在直角坐标系xoy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD或轴对称的△BC′D.
(1)当∠CBD=15°时,求点C′的坐标.
(2)当图1中的直线l经过点A,且k=﹣ ![]() 时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
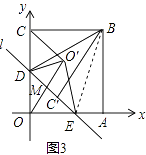
(3)当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作于△DOE或轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由.
【答案】
(1)
解:∵△CBD≌△C′BD,
∴∠CBD=∠C′BD=15°,C′B=CB=2,
∴∠CBC′=30°,
如图1,作C′H⊥BC于H,则C′H=1,HB= ![]() ,
,
∴CH=2﹣ ![]() ,
,
∴点C′的坐标为:(2﹣ ![]() ,1)
,1)
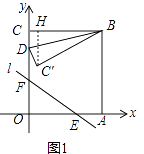
(2)
解:如图2,∵A(2,0),k=﹣ ![]() ,
,
∴代入直线AF的解析式为:y=﹣ ![]() x+b,
x+b,
∴b= ![]() ,
,
则直线AF的解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
∴∠OAF=30°,∠BAF=60°,
∵在点D由C到O的运动过程中,BC′扫过的图形是扇形,
∴当D与O重合时,点C′与A重合,
且BC′扫过的图形与△OAF重合部分是弓形,
当C′在直线y=﹣ ![]() x+
x+ ![]() 上时,BC′=BC=AB,
上时,BC′=BC=AB,
∴△ABC′是等边三角形,这时∠ABC′=60°,
∴重叠部分的面积是: ![]() ﹣
﹣ ![]() ×22=
×22= ![]() π﹣
π﹣ ![]()
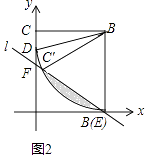
(3)
解:如图3,设OO′与DE交于点M,则O′M=OM,OO′⊥DE,
若△DO′E与△COO′相似,则△COO′必是Rt△,
在点D由C到O的运动过程中,△COO′中显然只能∠CO′O=90°,
∴CO′∥DE,
∴CD=OD=1,
∴b=1,
连接BE,由轴对称性可知C′D=CD,BC′=BC=BA,
∠BC′E=∠BCD=∠BAE=90°,
在Rt△BAE和Rt△BC′E中
∵ ![]() ,
,
∴Rt△BAE≌Rt△BC′E(HL),
∴AE=C′E,
∴DE=DC′+C′E=DC+AE,
设OE=x,则AE=2﹣x,
∴DE=DC+AE=3﹣x,
由勾股定理得:x2+1=(3﹣x)2,
解得:x=,
∵D(0,1),E( ![]() ,0),
,0),
∴ ![]() k+1=0,
k+1=0,
解得:k=﹣ ![]() ,
,
∴存在点D,使△DO′E与△COO′相似,这时k=﹣ ![]() ,b=1.
,b=1.
【解析】(1)利用翻折变换的性质得出∠CBD=∠C′BD=15°,C′B=CB=2,进而得出CH的长,进而得出答案;(2)首先求出直线AF的解析式,进而得出当D与O重合时,点C′与A重合,且BC′扫过的图形与△OAF重合部分是弓形,求出即可;(3)根据题意得出△DO′E与△COO′相似,则△COO′必是Rt△,进而得出Rt△BAE≌Rt△BC′E(HL),再利用勾股定理求出EO的长进而得出答案.
【考点精析】通过灵活运用确定一次函数的表达式和勾股定理的概念,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

【题目】为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出75m3的部分 | 2.5 |
超出75m3不超出125m3的部分 | a |
超出125m3的部分 | a+0.25 |

(1)若甲用户3月份的用气量为60m3 , 则应缴费元;
(2)若调价后每月支出的燃气费为y(元),每月的用气量为x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;
(3)在(2)的条件下,若乙用户2、3月份共用气175m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?