题目内容
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2 ![]() ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为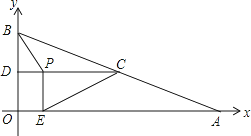
【答案】(1, ![]() )
)
【解析】解:∵点A、B的坐标分别为(8,0),(0,2 ![]() ) ∴BO=
) ∴BO= ![]() ,AO=8,由CD⊥BO,C是AB的中点,可得BD=DO=
,AO=8,由CD⊥BO,C是AB的中点,可得BD=DO= ![]() BO=
BO= ![]() =PE,CD=
=PE,CD= ![]() AO=4
AO=4
设DP=a,则CP=4﹣a
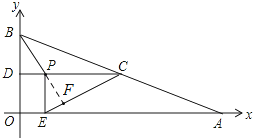
当BP所在直线与EC所在直线第一次垂直时,∠FCP=∠DBP
又∵EP⊥CP,PD⊥BD
∴∠EPC=∠PDB=90°
∴△EPC∽△PDB
∴ ![]() ,即
,即 ![]()
解得a1=1,a2=3(舍去)
∴DP=1
又∵PE= ![]() ∴P(1,
∴P(1, ![]() )
)
所以答案是:(1, ![]() ).
).
【考点精析】掌握平行线分线段成比例和相似三角形的判定与性质是解答本题的根本,需要知道三条平行线截两条直线,所得的对应线段成比例;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目