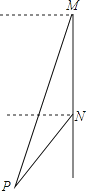��Ŀ����
����Ŀ��ͨ�����տư�ˣ��£��̲�һ��ϰ���̽���о�������֪����һ�κ���y=x��1��ͼ�����������������y=x��ͼ������ƽ��1����λ���ȵõ����Ƶģ����� ![]() ��ͼ�����ɷ���������
��ͼ�����ɷ��������� ![]() ��ͼ������ƽ��2����λ���ȵõ������������һ֪ʶ������⣮��ͼ����֪����������
��ͼ������ƽ��2����λ���ȵõ������������һ֪ʶ������⣮��ͼ����֪���������� ![]() ��ͼ��C������������y=ax��a��0����ͼ��l�ཻ�ڵ�A��2��2���͵�B��
��ͼ��C������������y=ax��a��0����ͼ��l�ཻ�ڵ�A��2��2���͵�B��
��1��д����B�����꣬����a��ֵ��
��2�������� ![]() ��ͼ���ֱ��ABͬʱ����ƽ��n��n��0������λ���ȣ��õ���ͼ��ֱ��ΪC���l�䣬��֪ͼ��C�侭����M��2��4����
��ͼ���ֱ��ABͬʱ����ƽ��n��n��0������λ���ȣ��õ���ͼ��ֱ��ΪC���l�䣬��֪ͼ��C�侭����M��2��4����
����n��ֵ��
�ڷֱ�д��ƽ�ƺ������ͼ��C���l���Ӧ�ĺ�����ϵʽ��
��ֱ��д������ʽ ![]() �Ľ⼯��
�Ľ⼯��
���𰸡�
��1��
�⣺��A��2��2������y=ax��2a=2�����a=1��
�߷��������� ![]() ��ͼ��������������y=x��ͼ��Ľ������ԭ��Գƣ�
��ͼ��������������y=x��ͼ��Ľ������ԭ��Գƣ�
��B����������2����2����
��2��
�⣺�ٺ��� ![]() ��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C��Ľ���ʽΪy=
��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C��Ľ���ʽΪy= ![]() ��
��
��M��2��4�������4= ![]() �����n=1��
�����n=1��
��ͼ��C��Ľ���ʽΪy= ![]() ��ͼ��l��Ľ���ʽΪy=x��1��
��ͼ��l��Ľ���ʽΪy=x��1��
�۲���ʽ ![]() �Ľ⼯�ǣ���1��x��1��x��3��
�Ľ⼯�ǣ���1��x��1��x��3��
����������1��ֱ�Ӱ�A���������y=ax�������a��ֵ�����÷�����������ͼ����������������ͼ��Ľ������ԭ��Գ�ȷ��B�����ꣻ��2���ٸ�������õ����� ![]() ��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C��Ľ���ʽΪy=
��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C��Ľ���ʽΪy= ![]() ��Ȼ���M��������뼴�ɵõ�n��ֵ���ڸ���������ͼ��C��Ľ���ʽΪy=
��Ȼ���M��������뼴�ɵõ�n��ֵ���ڸ���������ͼ��C��Ľ���ʽΪy= ![]() ��ͼ��l��Ľ���ʽΪy=x��1���۲���ʽ
��ͼ��l��Ľ���ʽΪy=x��1���۲���ʽ ![]() ������Ϊ�Ƚ�y=
������Ϊ�Ƚ�y= ![]() ��y=x��1�ĺ���ֵ������y=
��y=x��1�ĺ���ֵ������y= ![]() ��y=x��1Ϊ����
��y=x��1Ϊ���� ![]() ��ͼ���ֱ��ABͬʱ����ƽ��1����λ���ȣ��õ���ͼ������������
��ͼ���ֱ��ABͬʱ����ƽ��1����λ���ȣ��õ���ͼ������������ ![]() ��ͼ��������������y=ax��a��0����ͼ��Ľ���ΪA��2��2����B����2����2��������ƽ�ƺ�ֱ�Ϊ��3��2����B����1����2������1��x��1��x��3ʱ������y=
��ͼ��������������y=ax��a��0����ͼ��Ľ���ΪA��2��2����B����2����2��������ƽ�ƺ�ֱ�Ϊ��3��2����B����1����2������1��x��1��x��3ʱ������y= ![]() ��ͼ����y=x��1�ĺ���ͼ���·���
��ͼ����y=x��1�ĺ���ͼ���·���
�����㾫����������Ҫ�����˷����������ĸ���ͷ�����������ͼ������֪ʶ�㣬��Ҫ��������y��k/x��kΪ������k��0���ĺ�����Ϊ�������������Ա���x��ȡֵ��Χ��x������0��һ��ʵ����������ȡֵ��ΧҲ��һ�з���ʵ����������������ͼ������˫���ߣ�������������ͼ�������Գ�ͼ���������ĶԳ�ͼ�Σ��������Գ��ֱ��y=x�� y=-x���Գ������ǣ�ԭ�������ȷ�����⣮

 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�����Ŀ��Ϊ��Ԯ���ݡ��˺����š���ijУ�ٰ���һ���˺�֪ʶ����������10�֣�ѧ���÷�Ϊ�������ɼ��ﵽ6�����ϣ�����6�֣�Ϊ�ϸﵽ9�����ϣ�����9�֣�Ϊ���㣮��ξ����м�������ѧ���ɼ��ֲ�������ͳ��ͼ��ͼ��ʾ�� 
��1�������������ijɼ�ͳ�Ʒ�������
��� | ƽ���� | ��λ�� | ���� | �ϸ��� | ������ |
���� | 6.7 | 3.41 | 90% | 20% | |
���� | 7.5 | 1.69 | 80% | 10% |
��2��С��ͬѧ˵������ξ����ҵ���7�֣�������С����������������ƫ�ϣ����۲��ϱ���֪��С�������ѧ��������ס����ҡ���
��3������ͬѧ˵������ĺϸ��ʡ������ʾ��������飬����������ijɼ��������飮������ͬѧ��ͬ�����ͬѧ��˵������Ϊ������ijɼ�Ҫ���ڼ��飮�����������֧������ͬѧ�۵�����ɣ�