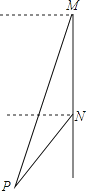题目内容
【题目】如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ= ![]() ,那么当点P运动一周时,点Q运动的总路程为 .
,那么当点P运动一周时,点Q运动的总路程为 . 
【答案】4
【解析】解:在Rt△AOB中,∵∠ABO=30°,AO=1,∴AB=2,BO= ![]() =
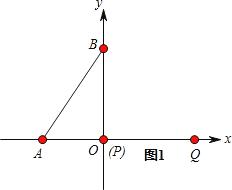
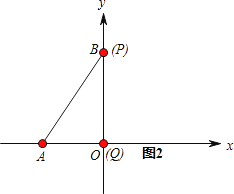
= ![]() ,①当点P从O→B时,如图1、图2所示,点Q运动的路程为
,①当点P从O→B时,如图1、图2所示,点Q运动的路程为 ![]() ,
,
②当点P从B→C时,如图3所示,这时QC⊥AB,则∠ACQ=90°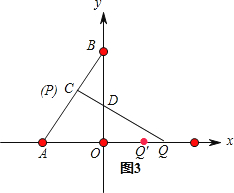
∵∠ABO=30°
∴∠BAO=60°
∴∠OQD=90°﹣60°=30°
∴cos30°= ![]() ∴AQ=
∴AQ= ![]() =2
=2
∴OQ=2﹣1=1
则点Q运动的路程为QO=1,
③当点P从C→A时,如图3所示,点Q运动的路程为QQ′=2﹣ ![]() ,
,
④当点P从A→O时,点Q运动的路程为AO=1,
∴点Q运动的总路程为: ![]() +1+2﹣
+1+2﹣ ![]() +1=4
+1=4
故答案为:4
本题主要是应用三角函数定义来解直角三角形,此题的解题关键是理解题意,正确画出图形;线段的两个端点看成是两个动点,将线段移动问题转化为点移动问题.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | M | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | N |
D.不知道 | 50 | 0.25 |

(1)根据上述统计图可得此次采访的人数为人,m= , n=
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人.
【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示. 
(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.