ЬтФПФкШн
ЁОЬтФПЁПдФЖСРэНтЃК
дВЪЧзюЭъУРЕФЭМаЮЃЌЫќОпгавЛаЉЬиЪтЕФаджЪЃКЭЌЛЁЛђЕШЛЁЫљЖдЕФдВжмНЧЯрЕШЃЌвЛЬѕЛЁЫљЖдЕФдВжмНЧЕШгкетЬѕЛЁЫљЖдЕФдВаФНЧЕФвЛАыЁЁЃЛЯШЙЙдьЁАИЈжњдВЁБЃЌдйРћгУдВЕФаджЪНЋЮЪЬтНјаазЊЛЏЃЌЭљЭљФмЛЏвўЮЊЯдЁЂЛЏФбЮЊвзЃЎ

НтОіЮЪЬтЃК
ШчЭМЃЌЕу![]() гыЕу
гыЕу![]() ЕФзјБъЗжБ№ЪЧ
ЕФзјБъЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧИУжБНЧзјБъЯЕФкЕФвЛИіЖЏЕуЃЎ
ЪЧИУжБНЧзјБъЯЕФкЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЪЙ![]() ЕФЕу
ЕФЕу![]() га_________ИіЃЛ
га_________ИіЃЛ
ЃЈ2ЃЉШєЕу![]() дк
дк![]() ЕФИКАыжсЩЯЃЌЧв
ЕФИКАыжсЩЯЃЌЧв![]() ЃЌЧѓТњзуЬѕМўЕФЕу
ЃЌЧѓТњзуЬѕМўЕФЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЕБ![]() ЮЊШёНЧЪБЃЌЩш
ЮЊШёНЧЪБЃЌЩш![]() ЃЌШєЕу
ЃЌШєЕу![]() дк
дк![]() жсЩЯвЦЖЏЪБЃЌТњзуЬѕМўЕФЕу
жсЩЯвЦЖЏЪБЃЌТњзуЬѕМўЕФЕу![]() га4ИіЃЌЧѓ
га4ИіЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЮоЪ§ЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
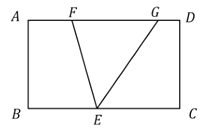
ЃЈ1ЃЉвдABЮЊБпзїГіЕШБпЁїABEКЭЁїABFЃЌЗжБ№вдЕуEЁЂFЮЊдВаФЃЌABЮЊАыОЖзїЁбEЁЂЁбFЃЌИљОндВжмНЧЖЈРэПЩжЊЃЌЪЙ![]() ЕФЕу
ЕФЕу![]() гаЮоЪ§ИіЃЛ
гаЮоЪ§ИіЃЛ
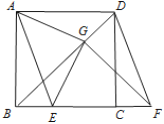
ЃЈ2ЃЉЙ§ЕуEзїEHЁЭyжсЃЌEGЁЭxжсЃЌДЙзуЗжБ№ЮЊHЁЂGЃЌСЌНгEC1ЃЌРћгУДЙОЖЖЈРэЧѓЕУAHЃНBHЃН3ЃЌдйИљОнОиаЮаджЪЕУEGЃНOHЃН5ЃЌOGЃНEHЃЌзюКѓРћгУЙДЙЩЖЈРэМЦЫуМДПЩЃЛ
ЃЈ3ЃЉИљОнТњзуЬѕМўЕФЕу![]() га4ИіПЩжЊЁбEЁЂЁбFгыxжсЯрНЛЃЌЕБЁбEгыxжсЯрЧагкЕуCЪБЃЌПЩЕУEBЃНECЃНOHЃН5ЃЌРћгУШ§НЧКЏЪ§ПЩЧѓЕУsinЁЯBEHЕФжЕЃЌдйИљОнДЙОЖЖЈРэМАдВжмНЧЖЈРэПЩЕУЁЯBEHЃНЁЯACBЃЌНјЖјПЩЧѓЕУЗћКЯЬтвтЕФ
га4ИіПЩжЊЁбEЁЂЁбFгыxжсЯрНЛЃЌЕБЁбEгыxжсЯрЧагкЕуCЪБЃЌПЩЕУEBЃНECЃНOHЃН5ЃЌРћгУШ§НЧКЏЪ§ПЩЧѓЕУsinЁЯBEHЕФжЕЃЌдйИљОнДЙОЖЖЈРэМАдВжмНЧЖЈРэПЩЕУЁЯBEHЃНЁЯACBЃЌНјЖјПЩЧѓЕУЗћКЯЬтвтЕФ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЌЁїABEКЭЁїABFЮЊЕШБпШ§НЧаЮЃЌЗжБ№вдЕуEЁЂFЮЊдВаФЃЌABЮЊАыОЖзїЁбEЁЂЁбFЃЌИљОндВжмНЧЖЈРэПЩжЊЃЌЯвABЫљЖдЕФгХЛЁЩЯЕФШЮвтвЛЕуCЖМЪЙ![]() ЃЌ
ЃЌ
ЁрЪЙ![]() ЕФЕу
ЕФЕу![]() гаЮоЪ§ИіЃЛ
гаЮоЪ§ИіЃЛ
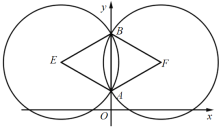
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуEзїEHЁЭyжсЃЌEGЁЭxжсЃЌДЙзуЗжБ№ЮЊHЁЂGЃЌСЌНгEC1ЃЌ

ЁпЕу![]() гыЕу
гыЕу![]() ЕФзјБъЗжБ№ЪЧ
ЕФзјБъЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
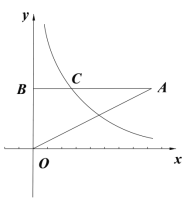
ЁрOAЃН2ЃЌOBЃН8ЃЌABЃН6ЃЌ
ЁпEHЁЭyжсЃЌ
ЁрAHЃНBHЃН3ЃЌ
ЁрOHЃНOAЃЋAHЃН2ЃЋ3ЃН5ЃЌ
ЁпEHЁЭyжсЃЌEGЁЭxжсЃЌxжсЁЭyжсЃЌ
ЁрЫФБпаЮEGOHЮЊОиаЮЃЌ
ЁрEGЃНOHЃН5ЃЌOGЃНEHЃЌ
ЁпABЃН6ЃЌЁїABEЮЊЕШБпШ§НЧаЮЃЌЕуC1дкЁбEЩЯ
ЁрEC1ЃНEAЃНABЃН6ЃЌ
дкRtЁїEAHжаЃЌEH![]() ЃЌ
ЃЌ
ЁрOGЃНEHЃН![]() ЃЌ
ЃЌ
дкRtЁїEC1GжаЃЌC1G![]() ЃЌ
ЃЌ
ЁрOC1ЃН OGЃЋ C1GЃН![]() ЃЌ
ЃЌ
ЁрЕуC1зјБъЮЊ![]() ЃЌ
ЃЌ
ЭЌРэПЩЕУЃКЕуC2зјБъЮЊ![]() ЃЌ
ЃЌ
ТњзуЬѕМўЕФЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМЃЌЕБЁбEгыxжсЯрЧагкЕуCЪБЃЌдђECЁЭxжсЃЌECЃНEBЃЌ

гжЁпEHЁЭyжсЃЌxжсЁЭyжсЃЌ
ЁрЫФБпаЮECOHЮЊОиаЮЃЌ
ЁрECЃНOHЃН5ЃЌ
ЁрEBЃНECЃН5ЃЌ
ЁрдкRtЁїEBHжаЃЌsinЁЯBEH![]() ЃЌ
ЃЌ
ЁпЁЯBEHЃН![]() ЁЯBEAЃЌЁЯACBЃН
ЁЯBEAЃЌЁЯACBЃН![]() ЁЯBEAЃЌ
ЁЯBEAЃЌ
ЁрЁЯACBЃНЁЯBEH
ЁрsinЁЯACBЃНsinЁЯBEH![]() ЃЌ
ЃЌ
ЁпЕБ![]() ЮЊШёНЧЪБЃЌТњзуЬѕМўЕФЕу
ЮЊШёНЧЪБЃЌТњзуЬѕМўЕФЕу![]() га4ИіЃЌ
га4ИіЃЌ
ЁрЁбEгыxжсЯрНЛЃЌ
ЁрsinЁЯACBЃМ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЕФШЁжЕЗЖЮЇЮЊЃК
ЕФШЁжЕЗЖЮЇЮЊЃК![]() ЃЎ
ЃЎ

 жЧЛлаЁИДЯАЯЕСаД№АИ
жЧЛлаЁИДЯАЯЕСаД№АИ