题目内容
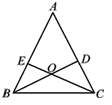
【题目】如图，
是等边三角形
内一点，将线段
绕点
顺时针旋转
得到线段
，连接
．若
，
，
，则四边形
的面积为（ ）
A.
B.
C.
D.
【答案】A
【解析】
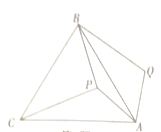
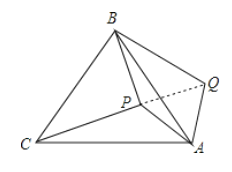
连结PQ，先根据等边三角形的性质和旋转的性质证明△APQ为等边三角形，则P Q=AP=6，再证明△APC≌△AQB,可得PC=QB=10，然后利用勾股定理的逆定理证明△PBQ为直角三角形，再根据三角形面积公式求出面积，最后利用S四边形APBQ=S△BPQ+S△APQ即可解答．
解：如图，连结PQ，
∵△ABC为等边三角形，
∴∠BAC=60°，AB=AC，
∵线段AP绕点A顺时针旋转60°得到线段AQ，
∴AP=PQ=6，∠PAQ=60°，
∴△APQ为等边三角形，
∴PQ=AP=6，
∵∠CAP+∠BAP=60°，∠BAP+∠BAQ=60°，
∴∠CAP=∠BAQ，
∵在△APC和△ABQ中，AC=AB，∠CAP=∠BAQ，AP=AQ
∴△APC≌△AQB，
∴PC=QB=10，
在△BPQ中， PB2=82=64，PQ2=62=36，BQ2=102=100，
∴PB2+PQ2=BQ2，
∴△PBQ为直角三角形，
∴∠BPQ=90°，
∴S四边形APBQ=S△BPQ+S△APQ=
×6×8+
×62=24+9
故答案为A．.
【题目】某文具商店销售学习用品，已知某品牌钢笔的进价是20元，销售过程发现，每月销量y支与销售单价x元（x为正整数）之间满足一次函数关系，且每支钢笔的售价不低于进价，也不高于35元，下表是y与x之间的对应数据：
销售单价x（元） | … | 22 | 24 | 30 | … |
月销量y（只） | … | 92 | 84 | 60 | … |
（1）求y与x的函数关系式并直接写出自变量x的取值范围.
（2）每支钢笔的售价定为多少元时，月销售利润恰为600元？
（3）每支钢笔的售价定为多少元时可使月销售利润最大？最大的月利润是多少？
