题目内容
【题目】已知函数y＝mx2﹣（2m+1）x+2（m≠0），请判断下列结论是否正确，并说明理由．
（1）当m＜0时，函数y＝mx2﹣（2m+1）x+2在x＞1时，y随x的增大而减小；
（2）当m＞0时，函数y＝mx2﹣（2m+1）x+2图象截x轴上的线段长度小于2．
【答案】（1）详见解析；（2）详见解析．
【解析】
（1）先确定抛物线的对称轴为直线x＝1+
，利用二次函数的性质得当m＞1+时，y随x的增大而减小，从而可对（1）的结论进行判断；
（2）设抛物线与x轴的两交的横坐标为x1、x2，则根据根与系数的关系得到x1+x2＝
，x1x2＝
，利用完全平方公式得到|x1﹣x2|＝
＝
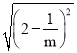＝|2﹣
|，然后m取
时可对（2）的结论进行判断．
解：（1）的结论正确．理由如下：
抛物线的对称轴为直线
，
∵m＜0，
∴当m＞1+时，y随x的增大而减小，
而1＞1+，
∴当m＜0时，函数y＝mx2﹣（2m+1）x+2在x＞1时，y随x的增大而减小；
（2）的结论错误．理由如下：
设抛物线与x轴的两交的横坐标为x1、x2，则x1+x2＝，x1x2＝，
|x1﹣x2|＝
＝
＝
＝
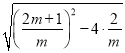
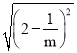
＝|2﹣|，
而m＞0，
若m取时，|x1﹣x2|＝3，
∴当m＞0时，函数y＝mx2﹣(2m+1)x+2图象截x轴上的线段长度小于2不正确．
练习册系列答案
名校课堂系列答案
相关题目
