题目内容
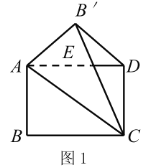
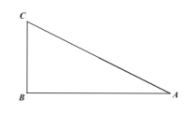
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() .将
.将![]() 绕点
绕点![]() 逆时针方向旋转,记旋转角为
逆时针方向旋转,记旋转角为![]() .
.

(1)问题发现
①当![]() 时,
时,![]() ____________;②当
____________;②当![]() 时,
时,![]() ___________.
___________.
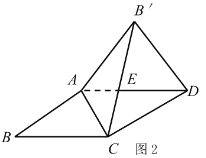
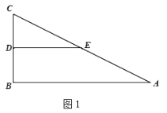
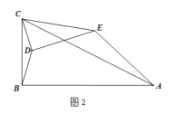
(2)拓展探究试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
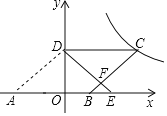
(3)问题解决
![]() 绕点
绕点![]() 逆时针旋转至
逆时针旋转至![]() 三点在同一条直线上时,直接写出线段
三点在同一条直线上时,直接写出线段![]() 的长.
的长.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() 的大小不变,证明见解析;(3)BD=
的大小不变,证明见解析;(3)BD=![]() 或
或![]()
【解析】
(1)①根据中点的定义和勾股定理求出BD、AC和AE,从而求出结论;
②画出图形,求出BD和AE即可求出结论;
(2)利用相似三角形的判定定理证出△ECA∽△DCB,从而证出结论;
(3)根据点E落在AB的延长线上和点E落在AB上分类讨论,分别画出对应的图形,然后求出AE的长,最后根据(2)的结论即可求出结论.
解:(1)①当![]() 时,
时,
∵在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,
的中点,
∴BD=CD=![]() ,AC=
,AC=![]() =
=![]()
∴AE=CE=![]()
∴![]()
![]()
![]()
故答案为:![]() ;
;
②当![]() 时,如下图所示
时,如下图所示
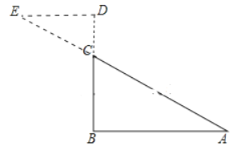
AE=AC+CE=![]() ,BD=BC+CD=6
,BD=BC+CD=6
∴![]()
![]()
![]()
故答案为:![]() ;
;
(2)当![]() 时,
时,![]() 的大小不变,证明如下
的大小不变,证明如下
![]()
![]()
∵![]()
∴△ECA∽△DCB
![]()
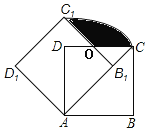
(3)(i)当点E落在AB的延长线上时,如下图所示
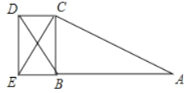
在Rt△BCE中,CE=![]() ,BC=4
,BC=4
BE=![]()
∴AE=AB+BE=10
∵![]()
∴BD=![]() ;
;
(ii)当点E落在AB上时,如下图所示
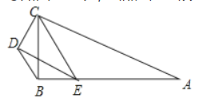
在Rt△BCE中,CE=![]() ,BC=4
,BC=4
BE=![]()
∴AE=AB-BE=6
∵![]()
∴BD=![]() ;
;
综上:BD=![]() 或
或![]() .
.

【题目】某文具商店销售学习用品,已知某品牌钢笔的进价是20元,销售过程发现,每月销量y支与销售单价x元(x为正整数)之间满足一次函数关系,且每支钢笔的售价不低于进价,也不高于35元,下表是y与x之间的对应数据:
销售单价x(元) | … | 22 | 24 | 30 | … |
月销量y(只) | … | 92 | 84 | 60 | … |
(1)求y与x的函数关系式并直接写出自变量x的取值范围.
(2)每支钢笔的售价定为多少元时,月销售利润恰为600元?
(3)每支钢笔的售价定为多少元时可使月销售利润最大?最大的月利润是多少?