题目内容
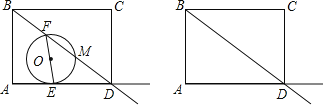
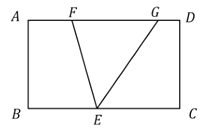
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上一动点,
边上一动点,![]() 、
、![]() 为
为![]() 边上两个动点,且
边上两个动点,且![]() ,则线段
,则线段![]() 的长度最大值为__________.
的长度最大值为__________.
【答案】![]()
【解析】
先作出△EFG的外接圆![]() ,过点O作OH⊥FG于点H,通过等腰直角三角形的转化可得到当
,过点O作OH⊥FG于点H,通过等腰直角三角形的转化可得到当![]() 的半径最大时,FG的长度取得最大值,进而可得到当
的半径最大时,FG的长度取得最大值,进而可得到当![]() 经过点B、D时,即点E、G分别与点B、D重合时,FG的长度取得最大值,设OH=HD=HF=x,利用Rt△BOE的勾股定理求解即可.
经过点B、D时,即点E、G分别与点B、D重合时,FG的长度取得最大值,设OH=HD=HF=x,利用Rt△BOE的勾股定理求解即可.
解:如图,作出△EFG的外接圆![]() ,过点O作OH⊥FG于点H,
,过点O作OH⊥FG于点H,

∵∠FEG=45°,
∴∠FOG=2∠FEG=90°,
又∵OG=OF,OH⊥FG,
∴FG=2HG=2OH,∠OFG=∠OGF=45°,
∵在Rt△OHG中,∠OGF=45°,
∴HG=![]() OG,
OG,
∴当![]() 的半径最大时,FG的长度取得最大值,
的半径最大时,FG的长度取得最大值,
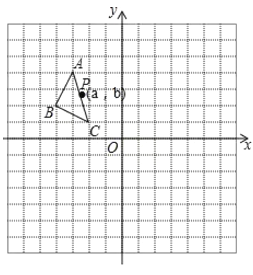
如下图,当![]() 经过点B、D时,即点E、G分别与点B、D重合时,FG的长度取得最大值,
经过点B、D时,即点E、G分别与点B、D重合时,FG的长度取得最大值,
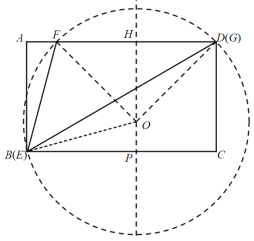
设OH=HD=HF=x,则OD=OB=![]() x,
x,
在矩形PCDH中,PC=DH=x,PH=CD=1,
∴BP=BC-PC=![]() -x,OP=PH-OH=1-x,
-x,OP=PH-OH=1-x,
在Rt△BOP中,BP2+OP2=BO2,
∴![]() ,
,
解得,![]() ,
,
∴FD=2x=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目