��Ŀ����
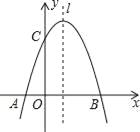
����Ŀ����֪������C��y��![]() ��ֱ��l��y��kx+b�ཻ�ڵ�A��B��ֱ��l��y�ύ�ڵ�P��
��ֱ��l��y��kx+b�ཻ�ڵ�A��B��ֱ��l��y�ύ�ڵ�P��
��1����k��0ʱ����![]() ��ֵ��
��ֵ��
��2����M���������ϵĶ��㣬����M��MG��ֱ��l�ڵ�G����k��0ʱ����![]() ��ֵ��
��ֵ��
��3����M���������ϵĶ��㣬����M��MG��y�ύֱ��l�ڵ�G����k��2ʱ����֤������bΪ��ʵ����![]() ��ֵΪ��ֵ������ֵ��
��ֵΪ��ֵ������ֵ��
��4��������2���������߸�Ϊ��y��ax2���������������䣬��![]() ��ֵ��Ϊ��ֵ�����ǣ��������ֵ�������ǣ�˵�����ɣ�
��ֵ��Ϊ��ֵ�����ǣ��������ֵ�������ǣ�˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3��֤������������ֵΪ
����3��֤������������ֵΪ![]() ����4��Ϊ��ֵ��
����4��Ϊ��ֵ��![]() ��|a|��
��|a|��
��������
��1�������������ֱ�ߵĽ������꣬��������빫ʽ����߶γ��ȣ���ɼ���![]() ��ֵ��
��ֵ��
��2����M������꣬�����������ֱ�ߵĽ������꣬��������빫ʽ����߶γ��ȣ�������������
��3����M������꣬�����������ֱ�ߵĽ������꣬��������빫ʽ����߶γ��ȣ�������������
��4������ǰ��Ľⷨ���м����ɣ�
�⣺��1����k��0ʱ��y��b��
��OP��|b|��
��![]() ��b��
��b��
��x����![]() b��
b��
��A����![]() b��b����B��
b��b����B��![]() b��b����
b��b����
��AB��2![]() b��
b��
��![]() ��
��![]() ��
��![]() ��
��
��2����k��0ʱ��y��b��
��M��x��![]() ����
����
��MG��ֱ��l��
��MG��|![]() ��b|��
��b|��
��A����![]() b��0����B��
b��0����B��![]() b��0����
b��0����
��GA��|x+![]() b|��GB��|x��
b|��GB��|x��![]() b|��
b|��
��![]() ��
��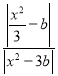 ��
��![]() ��
��
��3����k��2ʱ��y��2x+b��
��M��x��![]() ����
����
��MG��y�ᣬ
��G��x��2x+b����
��GM��|![]() ��2x��b|��
��2x��b|��![]() ��
��
�ⷽ����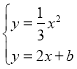 �ã�
�ã�
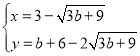 ��
��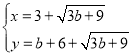
A��![]() ��
��![]() ����B��3+
����B��3+![]() ��b+6+
��b+6+![]() ����
����
��GA��![]() ��
��![]() ��
��
GB��![]() ��
��![]() ��
��
��GAGB��5|x2��6x��3b|��
��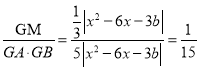 ��
��
��4���Ƕ�ֵ��
��k��0ʱ��y��b��
��M��x��ax2����
��MG��ֱ��l��
��MG��|ax2��b|��
�ⷽ����![]() �ã�
�ã�
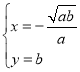 ��
��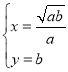 ��
��
��A����![]() ��b����B��
��b����B��![]() ��b����
��b����
��GA��|x+![]() |��GB��|x��
|��GB��|x��![]() |��
|��
��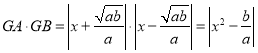 ��
��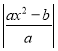
��![]() ��|a|Ϊ��ֵ��
��|a|Ϊ��ֵ��

 ��ʦ�㾦�ִʾ��ƪϵ�д�
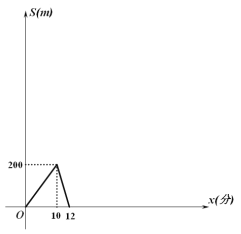
��ʦ�㾦�ִʾ��ƪϵ�д�����Ŀ��ij�ľ��̵�����ѧϰ��Ʒ����֪ijƷ�ƸֱʵĽ�����20Ԫ�����۹��̷��֣�ÿ������y֧�����۵���xԪ��xΪ��������֮������һ�κ�����ϵ����ÿ֧�ֱʵ��ۼ۲����ڽ��ۣ�Ҳ������35Ԫ���±���y��x֮��Ķ�Ӧ���ݣ�
���۵���x��Ԫ�� | �� | 22 | 24 | 30 | �� |
������y��ֻ�� | �� | 92 | 84 | 60 | �� |
��1����y��x�ĺ�����ϵʽ��ֱ��д���Ա���x��ȡֵ��Χ.
��2��ÿ֧�ֱʵ��ۼ���Ϊ����Ԫʱ������������ǡΪ600Ԫ��
��3��ÿ֧�ֱʵ��ۼ���Ϊ����Ԫʱ��ʹ������������������������Ƕ��٣�