题目内容
【题目】矩形ABCD中，AB=6，AD=8，点M在对角线AC上，且AM：MC=2：3，过点M作EF⊥AC交AD于点E，交BC于点F．在AC上取一点P，使∠MEP=∠EAC，则AP的长为_____．
【答案】
或
【解析】
由AB=6，AD=8，可得tan∠CAD=tan∠EAC=
,由∠MEP=∠EAC，可得
tan∠MEP= tan∠EAC=,在RT△MPE中，可求得ME、MP的值，可求得AP的长.
解：如图：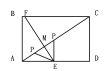
由AB=6，AD=8，可得AC=
,tan∠CAD=，
由AM：MC=2：3，可得AM=
,
过点M作EF⊥AC交AD于点E，交BC于点F,可得在RT△AME中，
ME=tan∠MAE
AM=
,
由∠MEP=∠EAC，可得在RT△MPE中，MP=MEtan∠MEP=3 
，
AP=AM-MP=4-
=,
或AP=AM+MP=4+=，
故答案：或.
练习册系列答案
阅读快车系列答案
相关题目
【题目】对垃圾进行分类投放，能有效提高对垃圾的处理和再利用，减少污染，保护环境.为了了解同学们对垃圾分类知识的了解程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识，某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取若干名同学进行了问卷测试，根据测试成绩分布情况，他们将全部测试成绩分成
、
、
、
四组，绘制了如下统计图表：
“垃圾分类知识及投放情况”问卷测试成绩统计图表
组别 | 分数/分 | 频数 | 各组总分/分 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
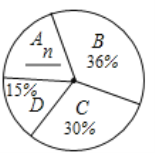
依据以上统计信息，解答下列问题：
（1）求得
_____，
______；
（2）这次测试成绩的中位数落在______组；
（3）求本次全部测试成绩的平均数．
