题目内容
【题目】在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题:
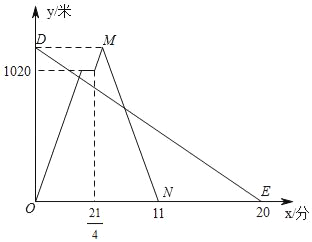
(1)请写出甲的骑行速度为 米/分,点M的坐标为 ;
(2)求甲返回时距A地的路程y与时间x之间的函数关系式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.
【答案】(1)240,(6,1200);(2)y=﹣240x+2640;(3)经过4分钟或6分钟或8分钟时两人距C地的路程相等.
【解析】
(1)根据函数图象得出AB两地的距离,由行程问题的数量关系由路程![]() 时间=速度就可以求出结论;
时间=速度就可以求出结论;
(2)先由行程问题的数量关系求出M、N的坐标,设y与x之间的函数关系式为y=kx+b,由待定系数法就可以求出结论;
(3) 设甲返回A地之前,经过x分两人距C地的路程相等,可得乙的速度:1200÷20=60(米/分),分别分①当0<x≤3时②当3<x<![]() ﹣1时③当
﹣1时③当![]() <x≤6时④当x=6时⑤当x>6时5种情况讨论可得经过多长时间两人距C地的路程相等.
<x≤6时④当x=6时⑤当x>6时5种情况讨论可得经过多长时间两人距C地的路程相等.
(1)由题意得:甲的骑行速度为: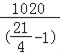 =240(米/分),
=240(米/分),
240×(11﹣1)÷2=1200(米),
则点M的坐标为(6,1200),
故答案为:240,(6,1200);
(2)设MN的解析式为:y=kx+b(k≠0),
∵y=kx+b(k≠0)的图象过点M(6,1200)、N(11,0),
∴![]() ,
,
解得![]() ,
,
∴直线MN的解析式为:y=﹣240x+2640;
即甲返回时距A地的路程y与时间x之间的函数关系式:y=﹣240x+2640;
(3)设甲返回A地之前,经过x分两人距C地的路程相等,
乙的速度:1200÷20=60(米/分),
![]()
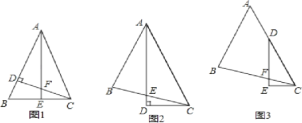
如图1所示:∵AB=1200,AC=1020,
∴BC=1200﹣1020=180,
分5种情况:
①当0<x≤3时,1020﹣240x=180﹣60x,
x=![]() >3,
>3,
此种情况不符合题意;
②当3<x<![]() ﹣1时,即3<x<
﹣1时,即3<x<![]() ,甲、乙都在A、C之间,
,甲、乙都在A、C之间,
∴1020﹣240x=60x﹣180,
x=4,
③当![]() <x≤6时,甲在B、C之间,乙在A、C之间,
<x≤6时,甲在B、C之间,乙在A、C之间,
∴240x﹣1020=60x﹣180,
x=![]() <
<![]() ,
,
此种情况不符合题意;
④当x=6时,甲到B地,距离C地180米,
乙距C地的距离:6×60﹣180=180(米),
即x=6时两人距C地的路程相等,
⑤当x>6时,甲在返回途中,
当甲在B、C之间时,180﹣[240(x﹣1)﹣1200]=60x﹣180,x=6,
此种情况不符合题意,
当甲在A、C之间时,240(x﹣1)﹣1200﹣180=60x﹣180,
x=8,
综上所述,在甲返回A地之前,经过4分钟或6分钟或8分钟时两人距C地的路程相等.