Question

【题目】（1）分解因式：．

（2）解不等式组：，并求它的整数解的和．

（3）解方程：．

Answer 1

【答案】（1）(m+3n+5)(m+3n-5)；（2）不等式的解集为-2＜x≤1，整数解的和为0；（3）x=1．

【解析】

（1）先利用完全平方公式分解，再利用平方差公式分解即可；

（2）分别求出两个不等式的解集，再找出两个解集的公共部分即可得不等式组的解集，进而得出整数解的和即可；

（3）先去分母，再移项，提取公因式，解方程即可求出x的值，最后检验是否有增根即可得答案．

（1）

=m2+6mn+9n2-25

=(m+3n)2-52

=(m+3n+5)(m+3n-5)．

（2），

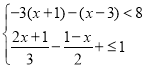解不等式-3(x+1)-(x-3)＜8得：x＞-2，

解不等式得：x≤1，

∴不等式的解集为：-2＜x≤1，

∴不等式的整数解为：-1，0，1，

∴不等式的整数解的和为：-1+0+1=0．

（3）

去分母得：x-2+4x-2(x+2)=(x+2)(x-2)，

移项，整理得：3(x-2)-(x+2)(x-2)=0，

∴(x-2)(1-x)=0，

解得：x1=2，x2=1，

检验：当x=2时，x2-4=0，故x=2不是原方程的解，

当x=1时，x2-4≠0，

∴x=1是原方程的解．