��Ŀ����
����Ŀ��ij�ؽ�����������Ϊ���˽���꼶ѧ��ÿѧ�ڲμ��ۺ�ʵ����������������������˸��ذ��꼶ѧ��һ��ѧ�ڲμ��ۺ�ʵ��������������õõ������ݻ���������������������ͳ��ͼ(��ͼ)��
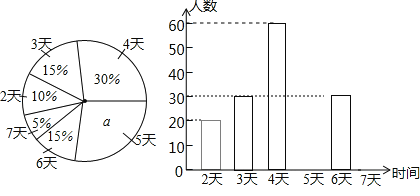
�������ͼ���ṩ����Ϣ���ش��������⣺
��1������μӳ�������İ��꼶ѧ������������Ƶ��ֱ��ͼ����������
��2������γ��������У���������λ���ֱ��Ƕ���?
��3��������ع��а��꼶ѧ��![]() �ˣ�������ơ��ʱ�䲻����
�ˣ�������ơ��ʱ�䲻����![]() �족�Ĵ�Լ�ж����ˣ�
�족�Ĵ�Լ�ж����ˣ�
���𰸡���1������ij�һѧ������200�ˣ���ͼ����������2����λ����4���죩��������4���죩����3�����ơ��ʱ�䲻����5�족�Ĵ�Լ��2700�ˣ�
��������
��1���ɲμ�ʵ���Ϊ2�������������ռ�İٷֱȼ���������꼶ѧ�����������ݵ�λ1��ȥ�����İٷֱ����a��ֵ����ѧ���������Իʵ����5����7��İٷֱ�������Ե���������ȫͳ��ͼ���ɣ�
��2�����ִ�����������Ϊ4�죬������Ϊ4����ʵ������������մ�С����˳�����У��ҳ����м���������������ƽ�������ɵõ���λ����
��3������ʱ�䲻����4��İٷֱ�֮�ͣ�����6000���ɵõ������
�⣺��1������ij�һѧ��������20��10%��200���ˣ���
���ʱ�䲻����5����������Ϊ��200����1-15%-10%-5%-15%-30%��=50���ˣ���
���ʱ�䲻����7����������Ϊ��200��5%=10���ˣ���
��ȫͳ��ͼ���£�
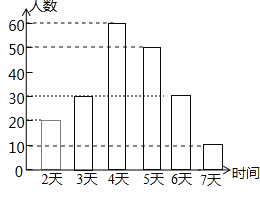
��2��������λ���ĸ����λ��Ӧ�ǵ�100�˵�������101�˵�������ƽ����������λ����4���죩��
���������ĸ��������������������������������4���죩��
��3���������ʱ�䲻����5�����Ĵ�Լ�У���200��20��30��60����200��6000��2700���ˣ���