Question

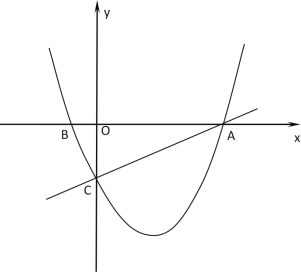
【题目】已知，点为二次函数图象的顶点，直线分别交轴的负半轴和轴于点，点．

(1)若二次函数图象经过点，求二次函数的解析式．

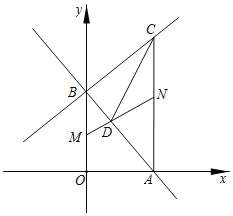
(2)如图，若点坐标为，且点在内部(不包含边界)．

①求的取值范围；

②若点，都在二次函数图象上，试比较与的大小

Answer 1

【答案】(1)；(2)①，②．

【解析】

(1)求出点B的坐标，代入二次函数解析式求出b的值，确定出二次函数解析式，进而求出m的值；
(2)①根据抛物线的顶点在△AOB的内部，确定b的取值范围；

②二次函数开口朝下，对称轴为，再根据点C(，y1)，D(，y2)的横坐标与对称轴的距离和抛物线的增减性进行判断．

(1)∵直线与y轴交于点B，

令，则，

∴点B的坐标为(0，2)，

将B(0，2)代入二次函数得：，

解得，

∴二次函数的解析式为；

(2)①∵点坐标为(-4，0)，

将A(-4，0)代入得：，

∴，

∴一次函数的解析式为，

∵二次函数图象的顶点为P(m，-2m+1)，点P在△AOB内部，

∴，解得；

②∵，

∴二次函数开口朝下，对称轴为，且，

又∵点C(，y1)，D(，y2)都在二次函数图象上，

点C和点D的横坐标中点为，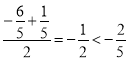

∴点C离对称轴比点D离对称轴远，开口朝下的抛物线上的点离对称轴越远的点对应的函数值越小，

∴．