题目内容
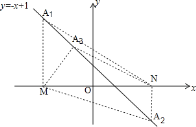
【题目】已知点M(-3,0),点N 是点M关于原点的对称点,点A是函数y= -x+1 图象上的一点,若△AMN是直角三角形,则点A的坐标为_______
【答案】(-3, 4),(3, -2)(![]() )或(
)或(![]() )
)
【解析】
分别过点M、N作x轴垂线与直线交点即为所求,由M、N点坐标可得点A坐标;在直线上取一点(x,-x+1),根据AM2+AN2=MN2列出关于x的方程,解方程可得第三种情况下点A的坐标.
解:①如图,过点M(-3,0)作x轴垂线交直线y=-x+1于点A1,则A1的坐标为(-3,4);
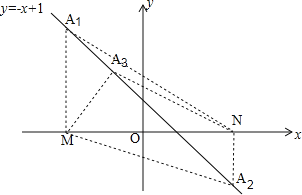
②过点N(3,0)作x轴垂线交直线y=-x+1于点A2,则A2的坐标为(3,-2);
③设直线y=-x+1上的点A3坐标为(x,-x+1),
根据题意,A3M2+A3N2=MN2,即(-3-x)2+(x-1)2+(3-x)2+(x-1)2=62,
整理,得:x2-4x-4=0,
解得:![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
∴点A3的坐标为(![]() )或(
)或(![]() ),
),
故答案为:(-3, 4),(3, -2)(![]() )或(
)或(![]() ).
).

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
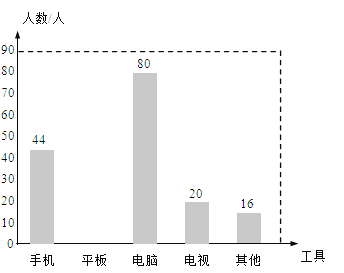
【题目】在“停课不停学”期间,某校数学兴趣小组对本校同学观看教学视频所使用的工具进行了调查,并从中随机抽取部分数据进行分析,将分析结果绘制成了两幅不完整的统计表与统计图.
工具 | 人数 | 频率 |
手机 | 44 | a |
平板 | b | 0.2 |
电脑 | 80 | c |
电视 | 20 | d |
不确定 | 16 | 0.08 |
请根据上述信息回答下列问题:
(1)所抽取出来的同学共 人,表中a= ,b= ;
(2)请补全条形统计图;
(3)若该校观看教学视频的学生总人数为2500人,则使用电脑的学生人数约 人.![]()