题目内容
【题目】如图,已知直线![]() 与x轴交于点C,与y轴交于点B,抛物线
与x轴交于点C,与y轴交于点B,抛物线![]() 经过B、C两点.
经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当![]() 面积最大时,请求出点E的坐标;
面积最大时,请求出点E的坐标;
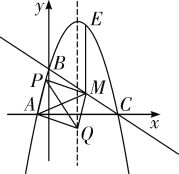
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 有最大值,此时
有最大值,此时![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)要求抛物线的解析式,先根据一次函数求点B和点C的坐标,再利用待定系数法求出二次函数的解析式;(2)要求当![]() 面积最大时,点E的坐标,首先过点E作
面积最大时,点E的坐标,首先过点E作![]() 轴,交直线BC于点G,设出点E的坐标,表示出点G的坐标,然后表示出EG的长,利用三角形面积公式及二次函数的最值即可得出点E的坐标;(3)要求使得以P、Q、A、M为顶点的四边形是平行四边形的点P的坐标,分三种情况:①以AM为边时,四边形AMQP是平行四边形;②以AM为边,四边形AMPQ是平行四边形;③以AM为对角线时,四边形APMQ是平行四边形,根据平行四边形的特征,即可求出点P的坐标.
轴,交直线BC于点G,设出点E的坐标,表示出点G的坐标,然后表示出EG的长,利用三角形面积公式及二次函数的最值即可得出点E的坐标;(3)要求使得以P、Q、A、M为顶点的四边形是平行四边形的点P的坐标,分三种情况:①以AM为边时,四边形AMQP是平行四边形;②以AM为边,四边形AMPQ是平行四边形;③以AM为对角线时,四边形APMQ是平行四边形,根据平行四边形的特征,即可求出点P的坐标.
解:(1)当![]() 时,
时,![]() ,∴
,∴![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
把![]() 和
和![]() 代入抛物线
代入抛物线![]() 中得:
中得: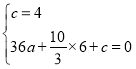 解得
解得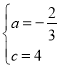 ,
,
∴抛物线的解析式为![]() ;
;
(2)如解图①,过点E作![]() 轴,交直线BC于点G.
轴,交直线BC于点G.
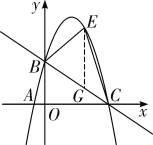 图①
图①
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值,∴此时
有最大值,∴此时![]() ;
;
(3)存在,点P的坐标是![]() 或
或![]() 或
或![]() .
.
[解法提示]
![]() ,
,
对称轴是直线![]() ,∴
,∴![]() ,
,
∵点Q是抛物线对称轴上的动点,∴点Q的横坐标为![]() ,
,
在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形;
①如解图②,以AM为边时,四边形AMQP是平行四边形,由(2)可得点M的横坐标是3,
∵点M在直线![]() 上,∴点M的坐标是
上,∴点M的坐标是![]() ,又∵点A的坐标是
,又∵点A的坐标是![]() ,点Q的横坐标为
,点Q的横坐标为![]() ,根据点M到点Q的平移规律可知点P的横坐标为
,根据点M到点Q的平移规律可知点P的横坐标为![]() ,∴
,∴![]() ;
;
②如解图③,以AM为边时,四边形AMPQ是平行四边形,
由(2)可得点M的横坐标是3,
∵![]() ,且点Q的横坐标为
,且点Q的横坐标为![]() ,
,
根据点A到点Q的平移规律可知点P的横坐标为![]() ,∴
,∴![]() ;
;
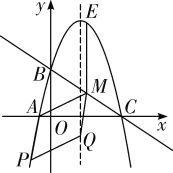 图②
图② 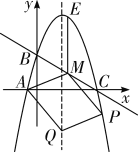 图③
图③
③如解图④,以AM为对角线时,四边形APMQ是平行四边形,根据点M到点Q的平移规律可得点P到点A的平移规律可知点P的横坐标为![]() ,∴
,∴![]() ;
;
 图④
图④
综上所述,在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,点P的坐标是![]() 或
或![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;

(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.