МвДїДЪИЭ
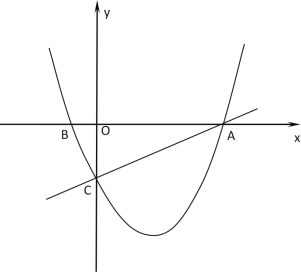
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬Ц±ПЯ![]() УлxЦбЅ»УЪµгAЈ¬УлyЦбЅ»УЪµгCЈ¬ЕЧОпПЯ
УлxЦбЅ»УЪµгAЈ¬УлyЦбЅ»УЪµгCЈ¬ЕЧОпПЯ![]() ѕ№эAЎўCБЅµгЈ¬УлxЦбµДБнТ»Ѕ»µгОЄµгBЈ®
ѕ№эAЎўCБЅµгЈ¬УлxЦбµДБнТ»Ѕ»µгОЄµгBЈ®
(1)ЗуЕЧОпПЯµДєЇКэ±нґпКЅЈ»
(2)µгDОЄЦ±ПЯACПВ·ЅЕЧОпПЯЙПТ»¶ЇµгЈ»
ўЩБ¬ЅУCDЈ¬КЗ·сґжФЪµгDЈ¬К№µГACЖЅ·ЦЎПOCDЈїИфґжФЪЈ¬ЗуµгDµДєбЧш±кЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
ўЪФЪўЩµДМхјюПВЈ¬ИфPОЄЕЧОпПЯЙПО»УЪACПВ·ЅµДТ»ёц¶ЇµгЈ¬ТФPЎўCЎўAЎўDОЄ¶ҐµгµДЛД±ЯРОГж»эјЗЧчSЈ¬ФтSИЎєОЦµ»тФЪКІГґ·¶О§К±Ј¬ПаУ¦µДµгPУРЗТЦ»УР2ёцЈї
Ўѕґр°ёЎї(1)![]() Ј»(2)ўЩґжФЪЈ¬µг
Ј»(2)ўЩґжФЪЈ¬µг![]() µДєбЧш±кОЄ
µДєбЧш±кОЄ![]() Ј»ўЪ
Ј»ўЪ![]()
ЎѕЅвОцЎї
ЈЁ1Ј©ПИЗуіцµгAЎўCЧш±кЈ¬ФЩёщѕЭґэ¶ЁПµКэ·ЁЗуЅвјґїЙЈ»
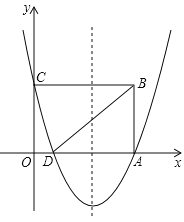
ЈЁ2Ј©ўЩИфґжФЪµгDЈ¬К№µГACЖЅ·ЦЎПOCDЈ¬ФтЎПOCA=ЎПDCAЈ¬№эµгDЧчDEЎНxЦбУЪµгEЈ¬Ѕ»Ц±ПЯACУЪµгFЈ¬ИзНј1Ј¬ФтDEЎОyЦбЈ¬ТЧµГDC=DFЈ¬ЙиDЈЁmЈ¬![]() Ј©Ј¬ФтїЙУГє¬mµДґъКэКЅ±нКѕіцDFЈ¬И»єуёщѕЭDC=DFјґїЙµГіц№ШУЪmµД·ЅіМЈ¬Ѕв·ЅіМјґµГЅб№ыЈ»
Ј©Ј¬ФтїЙУГє¬mµДґъКэКЅ±нКѕіцDFЈ¬И»єуёщѕЭDC=DFјґїЙµГіц№ШУЪmµД·ЅіМЈ¬Ѕв·ЅіМјґµГЅб№ыЈ»
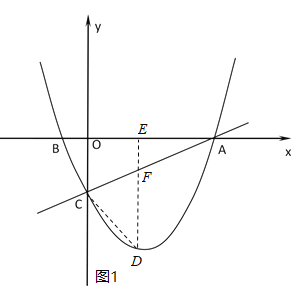
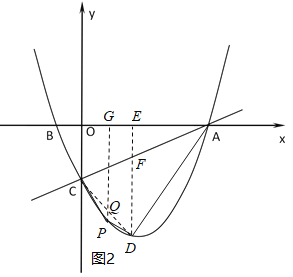
ўЪПИУЙўЩµДЅбВЫЗуіцµгDµДЧш±кєНЎчACDµДГж»эЈ¬И»єу·ЦµгPФЪЦ±ПЯCDПВ·ЅК±Ј¬ЧчPGЎНxЦбУЪµгGЈ¬Ѕ»Ц±ПЯCDУЪµгQЈ¬ИзНј2Ј¬АыУГ¶юґОєЇКэµДРФЦКЗуіцЎчPCDµДЧоґуГж»эЈ¬ЅшТ»ІЅјґїЙЗуіцУРИэёцµгPК±µДSµДЦµЈ»µгPФЪЦ±ПЯADПВ·ЅК±Ј¬ёЁЦъПЯЧч·ЁИзНј3Ј¬ФЩЗуіцЎчPADµДЧоґуГж»эЈ¬Ѕш¶шїЙЗуіцЦ»УРТ»ёцµгPК±µДSµДЦµЈ¬УЪКЗїЙµГЅб№ыЈ®
ЅвЈєЈЁ1Ј©¶Ф![]() Ј¬µ±y=0К±Ј¬x=4Ј¬ЎаµгAЈЁ4Ј¬0Ј©Ј¬
Ј¬µ±y=0К±Ј¬x=4Ј¬ЎаµгAЈЁ4Ј¬0Ј©Ј¬
µ±x=0К±Ј¬y=©Ѓ2Ј¬ЎаµгCЈЁ0Ј¬©Ѓ2Ј©Ј¬
°СAЎўCБЅµгґъИлЕЧОпПЯ![]() µГЈє
µГЈє
![]() Ј¬ЅвµГЈє
Ј¬ЅвµГЈє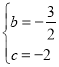 Ј¬
Ј¬
ЎаЕЧОпПЯµДЅвОцКЅКЗ![]() Ј»
Ј»
ЈЁ2Ј©ўЩИфґжФЪµгDЈ¬К№µГACЖЅ·ЦЎПOCDЈ¬ФтЎПOCA=ЎПDCAЈ¬
№эµгDЧчDEЎНxЦбУЪµгEЈ¬Ѕ»Ц±ПЯACУЪµгFЈ¬ИзНј1Ј¬ФтDEЎОyЦбЈ¬
ЎаЎПOCA=ЎПDFCЈ¬ЎаЎПDCF=ЎПDFCЈ¬ЎаDC=DFЈ¬
ЙиDЈЁmЈ¬![]() Ј©Ј¬ФтFЈЁmЈ¬
Ј©Ј¬ФтFЈЁmЈ¬![]() Ј©Ј¬
Ј©Ј¬
Ўа![]() Ј¬
Ј¬
Ўа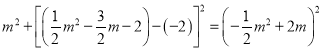 Ј¬
Ј¬
ЅвµГЈє![]() ЈЁЙбИҐЈ©»т
ЈЁЙбИҐЈ©»т![]() Ј¬
Ј¬
ЎаґжФЪµгDЈ¬К№µГACЖЅ·ЦЎПOCDЈ¬ЗТµгDµДєбЧш±кКЗ![]() Ј»
Ј»
ЈЁ3Ј©¶Ф![]() Ј¬µ±x=
Ј¬µ±x=![]() К±Ј¬
К±Ј¬![]() Ј¬ЎаµгDµДЧш±кКЗЈЁ
Ј¬ЎаµгDµДЧш±кКЗЈЁ![]() Ј¬
Ј¬![]() Ј©Ј¬
Ј©Ј¬
ґЛК±DF=![]() Ј¬ЎчACDµДГж»э=
Ј¬ЎчACDµДГж»э=![]() Ј¬
Ј¬
µ±µгPФЪЦ±ПЯCDПВ·ЅК±Ј¬ЧчPGЎНxЦбУЪµгGЈ¬Ѕ»Ц±ПЯCDУЪµгQЈ¬ИзНј2Ј¬
ЎЯµгCЈЁ0Ј¬©Ѓ2Ј©Ј¬DЈЁ![]() Ј¬
Ј¬![]() Ј©Ј¬
Ј©Ј¬
ЎаЦ±ПЯCDµДЅвОцКЅОЄ![]() Ј¬
Ј¬
ЙиµгPµДЧш±кКЗЈЁnЈ¬![]() Ј©Ј¬ФтQЈЁnЈ¬
Ј©Ј¬ФтQЈЁnЈ¬![]() Ј©Ј¬
Ј©Ј¬
Ўа![]() Ј¬
Ј¬
ЎаЎчPCDµДЧоґуГж»э=![]() Ј¬
Ј¬
ґЛК±ЛД±ЯРОCPDAµДГж»э=![]() Ј»
Ј»
µ±µгPФЪЦ±ПЯADПВ·ЅК±Ј¬ЧчPGЎНxЦбУЪµгGЈ¬Ѕ»Ц±ПЯCDУЪµгQЈ¬ИзНј3Ј¬
ЎЯµгAЈЁ4Ј¬0Ј©Ј¬DЈЁ![]() Ј¬
Ј¬![]() Ј©Ј¬
Ј©Ј¬
ЎаЦ±ПЯADµДЅвОцКЅОЄ![]() Ј¬
Ј¬
ЙиµгPµДЧш±кКЗЈЁnЈ¬![]() Ј©Ј¬ФтQЈЁnЈ¬
Ј©Ј¬ФтQЈЁnЈ¬![]() Ј©Ј¬
Ј©Ј¬
Ўа![]() Ј¬
Ј¬
ЎаЎчPADµДЧоґуГж»э=![]() Ј¬
Ј¬
ґЛК±ЛД±ЯРОCDPAµДГж»э=![]() Ј»
Ј»
ЧЫЙПЈ¬µ±SµДИЎЦµ·¶О§ОЄ![]() Ј¬ПаУ¦µДµгPУРЗТЦ»УР2ёцЈ®
Ј¬ПаУ¦µДµгPУРЗТЦ»УР2ёцЈ®


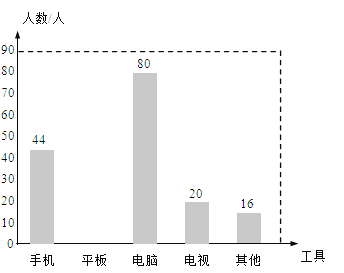
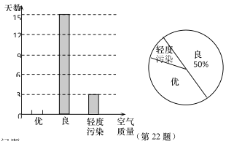
ЎѕМвДїЎїФЪЎ°НЈїОІ»НЈС§Ў±ЖЪјдЈ¬ДіРЈКэС§РЛИ¤РЎЧй¶Ф±ѕРЈН¬С§№ЫїґЅМС§КУЖµЛщК№УГµД№¤ѕЯЅшРРБЛµчІйЈ¬ІўґУЦРЛж»ъійИЎІї·ЦКэѕЭЅшРР·ЦОцЈ¬Ѕ«·ЦОцЅб№ы»жЦЖіЙБЛБЅ·щІ»НкХыµДНіјЖ±нУлНіјЖНјЈ®
№¤ѕЯ | ИЛКэ | ЖµВК |
КЦ»ъ | 44 | a |
ЖЅ°е | b | 0.2 |
µзДФ | 80 | c |
µзКУ | 20 | d |
І»И·¶Ё | 16 | 0.08 |
ЗлёщѕЭЙПКцРЕПў»ШґрПВБРОКМвЈє
ЈЁ1Ј©ЛщійИЎіцАґµДН¬С§№ІЎЎ ЎЎИЛЈ¬±нЦРaЈЅЎЎ ЎЎЈ¬bЈЅЎЎ ЎЎЈ»
ЈЁ2Ј©ЗлІ№И«МхРОНіјЖНјЈ»
ЈЁ3Ј©ИфёГРЈ№ЫїґЅМС§КУЖµµДС§ЙъЧЬИЛКэОЄ2500ИЛЈ¬ФтК№УГµзДФµДС§ЙъИЛКэФјЎЎ ЎЎИЛЈ®![]()