题目内容
【题目】如图,![]() 是
是![]() 的中线,且
的中线,且![]() ,将
,将![]() 绕点
绕点![]() 旋转
旋转![]() 得到
得到![]() ,则
,则![]() _______
_______![]() .
.![]() 的面积_________
的面积_________![]() .
.
【答案】2 18
【解析】
根据![]() 是
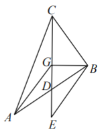
是![]() 的中线,且CG=2DG可得点G为△ABC的重心,得到CD=3GD=6,DE=GD=
的中线,且CG=2DG可得点G为△ABC的重心,得到CD=3GD=6,DE=GD=![]() GC=2,再利用勾股定理逆定理证明BG⊥CE,根据中线的性质,得S△ACD=S△BCD,可求△BCD的面积.
GC=2,再利用勾股定理逆定理证明BG⊥CE,根据中线的性质,得S△ACD=S△BCD,可求△BCD的面积.
解:∵![]() 是
是![]() 的中线,且CG=2DG,
的中线,且CG=2DG,
∴点G为△ABC的重心,
∴CD=3GD=6,
根据旋转的性质得:DE=GD=![]() GC=2,
GC=2,
∵GB=3,EG=GC=4,BE=GA=5,
∴BG2+GE2=BE2,即BG⊥CE,
∵CD为△ABC的中线,
∴S△ACD=S△BCD,
∴S△ABC=S△ACD+S△BCD=2S△BCD=2×![]() ×BG×CD=18cm2.
×BG×CD=18cm2.
故答案为:2,18.

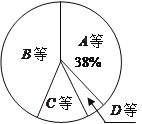
【题目】某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成下面的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
D | 5分以下 | 3 | 0.06 |
合计 | 50 | 1.00 |
(1)试直接写出
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
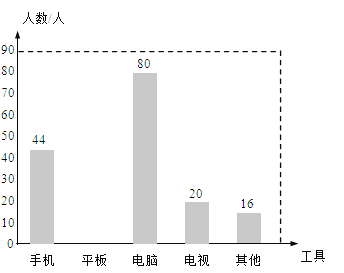
【题目】在“停课不停学”期间,某校数学兴趣小组对本校同学观看教学视频所使用的工具进行了调查,并从中随机抽取部分数据进行分析,将分析结果绘制成了两幅不完整的统计表与统计图.
工具 | 人数 | 频率 |
手机 | 44 | a |
平板 | b | 0.2 |
电脑 | 80 | c |
电视 | 20 | d |
不确定 | 16 | 0.08 |
请根据上述信息回答下列问题:
(1)所抽取出来的同学共 人,表中a= ,b= ;
(2)请补全条形统计图;
(3)若该校观看教学视频的学生总人数为2500人,则使用电脑的学生人数约 人.![]()