题目内容
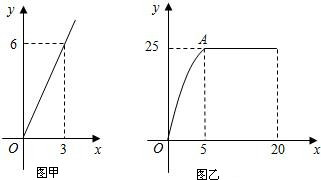
某公司推出一款新型手机,投放市场以来前3个月的利润情况如图所示,该图可以近似看作抛物线的一部分.请结合图象,解答以下问题:
(1)求该抛物线对应的二次函数解析式;
(2)该公司在经营此款手机过程中,第几月的利润能达到24万元?
(3)若照此经营下去,请你结合所学的知识,对公司在此款手机的经营状况(是否亏损?何时亏损?)作预测分析.
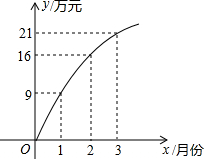
(1)求该抛物线对应的二次函数解析式;
(2)该公司在经营此款手机过程中,第几月的利润能达到24万元?
(3)若照此经营下去,请你结合所学的知识,对公司在此款手机的经营状况(是否亏损?何时亏损?)作预测分析.

(1)设二次函数解析式为y=ax2+bx+c,
根据图象,
,
解得
,
所以,该抛物线对应的二次函数解析式为y=-x2+10x;
(2)当利润y=24万时,-x2+10x=24,
整理得,x2-10x+24=0,
解得x1=4,x2=6,
所以,从第4个月到第6个月,即第4个月、第5个月、第6个月的利润能达到24万元;
(3)y=-x2+10x=-(x-5)2+25,
令y=0,-x2+10x=0,
解得x1=0,x2=10,
所以,第1个月到第5个月,利润逐渐增加,第5个月到第10个月利润逐渐减小,但是前10个月都是盈利,从第11个月开始亏损.
根据图象,
|
解得
|
所以,该抛物线对应的二次函数解析式为y=-x2+10x;
(2)当利润y=24万时,-x2+10x=24,
整理得,x2-10x+24=0,
解得x1=4,x2=6,
所以,从第4个月到第6个月,即第4个月、第5个月、第6个月的利润能达到24万元;
(3)y=-x2+10x=-(x-5)2+25,
令y=0,-x2+10x=0,
解得x1=0,x2=10,
所以,第1个月到第5个月,利润逐渐增加,第5个月到第10个月利润逐渐减小,但是前10个月都是盈利,从第11个月开始亏损.

练习册系列答案
相关题目