题目内容
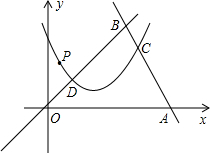
如图所示，己知点P是x轴上一点，以P为圆心的⊙P分别与x轴、y轴交于点A、B和C、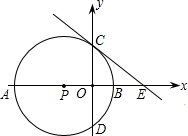
D，其中A（-3，0），B（1，0）．过点C作⊙P的切线交x轴于点E．
（1）求直线CE的解析式；
（2）求过A、B、C三点的抛物线解析式；
（3）第（2）问中的抛物线的顶点是否在直线CE上，请说明理由；
（4）点F是线段CE上一动点，点F的横坐标为m，问m在什么范围内时，直线FB与⊙P相交？
D，其中A（-3，0），B（1，0）．过点C作⊙P的切线交x轴于点E．（1）求直线CE的解析式；
（2）求过A、B、C三点的抛物线解析式；
（3）第（2）问中的抛物线的顶点是否在直线CE上，请说明理由；
（4）点F是线段CE上一动点，点F的横坐标为m，问m在什么范围内时，直线FB与⊙P相交？
（1）连接PC，OC=
=
，
∵cos∠CPO=PO：PC=1：2
∴∠CPO=60°，
∴PE=4，
∴OE=3，
c（0，
），E（3，0）．
设直线CE的解析式为y=kx+b，
b=
，3k+b=0，
解得k=-
x，
∴y=-
+
．
（2）设抛物线解析式为y=a（x+3）（x-1）
∵点C（0，
）在图象上，
代入得a=-
∴y=-
（x+3）（x-1）．
（3）抛物线顶点为（-1，
），
当x=-1时，代入直线CE解析式y=
，
故（2）中抛物线顶点在直线CE上．
（4）当FB与OE垂直时，FB切⊙P于B，此时m=1．
而点F在线段CE其他位置时，FB都与⊙P相交．
故0≤m≤3且m≠1．
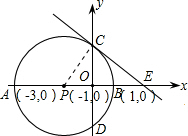
| 22-12 |
| 3 |
∵cos∠CPO=PO：PC=1：2
∴∠CPO=60°，
∴PE=4，
∴OE=3，
c（0，
| 3 |
设直线CE的解析式为y=kx+b，
b=
| 3 |
解得k=-
| ||
| 3 |
∴y=-
| ||
| 3 |
| 3 |
（2）设抛物线解析式为y=a（x+3）（x-1）
∵点C（0，
| 3 |
代入得a=-
| ||
| 3 |
∴y=-
| ||
| 3 |
（3）抛物线顶点为（-1，
4
| ||
| 3 |
当x=-1时，代入直线CE解析式y=
4
| ||
| 3 |
故（2）中抛物线顶点在直线CE上．
（4）当FB与OE垂直时，FB切⊙P于B，此时m=1．
而点F在线段CE其他位置时，FB都与⊙P相交．
故0≤m≤3且m≠1．
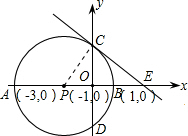
练习册系列答案
相关题目
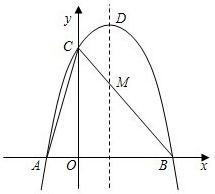
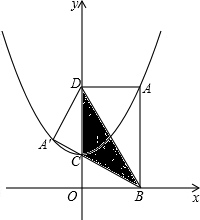
点C，顶点为D．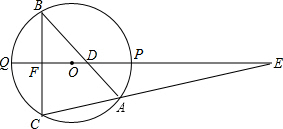
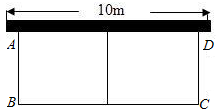篱笆，一面靠墙（墙长为10m），设花圃宽AB为x（m），面积为S（m2）．