题目内容
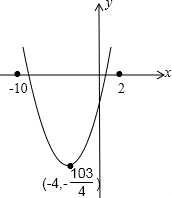
在平面直角坐标系中,横坐标与纵坐标都是整数的点(x,y)称为整点,如果将二次函数y=x2+8x-
的图象与x轴所围成的封闭图形染成红色,则此红色区域内部及其边界上的整点个数有______个.
| 39 |
| 4 |
由二次函数y=x2+8x-
,得y=(x+4)2-
,
顶点为(-4,-
).
令y=0,则x=-4-
≈-9.07或x=-4+
≈1.07,
故在红色区域内部及其边界上的整点有:
(-9,0),(-8,0),(-7,0),(-6,0),(-5,0),(-4,0),(-3,0),(-2,0),(-1,0),(0,0),(1,0),共11个;
(-8,-1),(-8,-2),…,(-8,-9),共9个;
(-7,-1),(-7,-2),…,(-7,-16),共16个;
(-6,-1),(-6,-2),…,(-6,-21),共21个;
(-5,-1),(-5,-2),…,(-5,-24),共24个;
(-4,-1),(-4,-2),…,(-4,-25),共25个;
由对称性,可知(-3,-1),(-3,-2),…,(-3,-24),共24个;
(-2,-1),(-2,-2),…,(-2,-21),共21个;
(-1,-1),(-1,-2),…,(-1,-16),共16个;
(0,-1),(0,-2),…,(0,-9),共9个;
一共11+2(9+16+21+24)+25=176个,
故答案为:176.
| 39 |
| 4 |
| 103 |
| 4 |
顶点为(-4,-
| 103 |
| 4 |
令y=0,则x=-4-
| ||
| 2 |
| ||
| 2 |
故在红色区域内部及其边界上的整点有:
(-9,0),(-8,0),(-7,0),(-6,0),(-5,0),(-4,0),(-3,0),(-2,0),(-1,0),(0,0),(1,0),共11个;
(-8,-1),(-8,-2),…,(-8,-9),共9个;
(-7,-1),(-7,-2),…,(-7,-16),共16个;
(-6,-1),(-6,-2),…,(-6,-21),共21个;
(-5,-1),(-5,-2),…,(-5,-24),共24个;
(-4,-1),(-4,-2),…,(-4,-25),共25个;
由对称性,可知(-3,-1),(-3,-2),…,(-3,-24),共24个;
(-2,-1),(-2,-2),…,(-2,-21),共21个;
(-1,-1),(-1,-2),…,(-1,-16),共16个;
(0,-1),(0,-2),…,(0,-9),共9个;
一共11+2(9+16+21+24)+25=176个,
故答案为:176.


练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
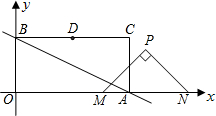 点作等腰直角三角形PMN,点P在第一象限,设矩形OACB与△PMN重叠部分的面积为S.
点作等腰直角三角形PMN,点P在第一象限,设矩形OACB与△PMN重叠部分的面积为S.

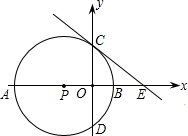 D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E.
D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E.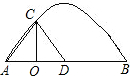 的坐标(坐标轴上的一个长度单位为1m);
的坐标(坐标轴上的一个长度单位为1m);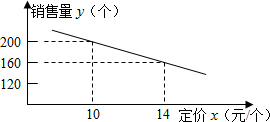 个星期的销售量y(个)与它的定价x(元/个)的关系如图所示:
个星期的销售量y(个)与它的定价x(元/个)的关系如图所示: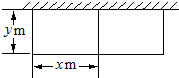
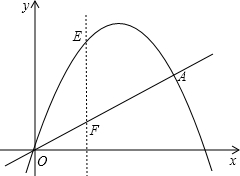 x的图象交于O、A两点.
x的图象交于O、A两点.