题目内容
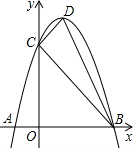
如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于 点C,顶点为D.
点C,顶点为D.
(1)直接写出抛物线的对称轴,及抛物线与x轴的另一个交点A的坐标;
(2)以AD为直径的圆经过点C.
①求抛物线的解析式;
②点E在抛物线的对称轴上,点F在抛物线上,且以B,A,F,E四点为顶点的四边形为平行四边形,求点F的坐标.
 点C,顶点为D.
点C,顶点为D.(1)直接写出抛物线的对称轴,及抛物线与x轴的另一个交点A的坐标;
(2)以AD为直径的圆经过点C.
①求抛物线的解析式;
②点E在抛物线的对称轴上,点F在抛物线上,且以B,A,F,E四点为顶点的四边形为平行四边形,求点F的坐标.
(1)对称轴是直线:x=1,
点A的坐标是(3,0);
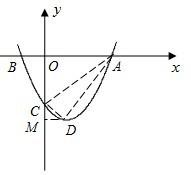
(2)①如图,连接AC、AD,过D作DM⊥y轴于点M,
解法一:利用△AOC∽△CMD,
在y=ax2-2ax-b(a>0)中,当x=1时,y=-a-b,则D的坐标是(1,-a-b).
∵点A、D、C的坐标分别是A(3,0),D(1,-a-b)、
C(0,-b),
∴AO=3,MD=1.
由
=
,
得
=
,
∴3-ab=0.(3分)
又∵0=a•(-1)2-2a•(-1)-b,(4分)
∴由
,
得
,(5分)
∴函数解析式为:y=x2-2x-3.(6分)
解法二:利用以AD为直径的圆经过点C,
∵点A、D的坐标分别是A(3,0)、D(1,-a-b)、C(0,-b),
∴AC=
,CD=
,AD=
∵AC2+CD2=AD2
∴3-ab=0①(3分)
又∵0=a•(-1)2-2a•(-1)-b②(4分)
由①、②得a=1,b=3(5分)
∴函数解析式为:y=x2-2x-3.(6分)
②F点存在.
如图所示,当四边形BAFE为平行四边形时
则BA∥EF,并且BA=EF.
∵BA=4,
∴EF=4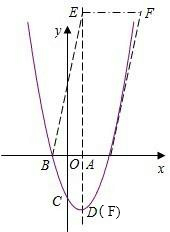
由于对称轴为x=1,
∴点F的横坐标为5.(7分)
将x=5代入y=x2-2x-3得y=12,∴F(5,12).(8分)
根据抛物线的对称性可知,在对称轴的左侧抛物线上也存在点F,
使得四边形BAEF是平行四边形,此时点F坐标为(-3,12).(9分)
当四边形BEAF是平行四边形时,点F即为点D,
此时点F的坐标为(1,-4).(10分)
综上所述,点F的坐标为(5,12),(-3,12)或(1,-4).
点A的坐标是(3,0);
(2)①如图,连接AC、AD,过D作DM⊥y轴于点M,
解法一:利用△AOC∽△CMD,
在y=ax2-2ax-b(a>0)中,当x=1时,y=-a-b,则D的坐标是(1,-a-b).
∵点A、D、C的坐标分别是A(3,0),D(1,-a-b)、
C(0,-b),
∴AO=3,MD=1.
由
| AO |
| CM |
| OC |
| MD |
得
| 3 |
| a |
| b |
| 1 |

∴3-ab=0.(3分)
又∵0=a•(-1)2-2a•(-1)-b,(4分)
∴由
|
得
|
∴函数解析式为:y=x2-2x-3.(6分)
解法二:利用以AD为直径的圆经过点C,
∵点A、D的坐标分别是A(3,0)、D(1,-a-b)、C(0,-b),
∴AC=
| 9+b2 |
| 1+a2 |
| 4+(-a-b)2 |
∵AC2+CD2=AD2
∴3-ab=0①(3分)
又∵0=a•(-1)2-2a•(-1)-b②(4分)
由①、②得a=1,b=3(5分)
∴函数解析式为:y=x2-2x-3.(6分)
②F点存在.
如图所示,当四边形BAFE为平行四边形时
则BA∥EF,并且BA=EF.
∵BA=4,
∴EF=4

由于对称轴为x=1,
∴点F的横坐标为5.(7分)
将x=5代入y=x2-2x-3得y=12,∴F(5,12).(8分)
根据抛物线的对称性可知,在对称轴的左侧抛物线上也存在点F,
使得四边形BAEF是平行四边形,此时点F坐标为(-3,12).(9分)
当四边形BEAF是平行四边形时,点F即为点D,
此时点F的坐标为(1,-4).(10分)
综上所述,点F的坐标为(5,12),(-3,12)或(1,-4).

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目

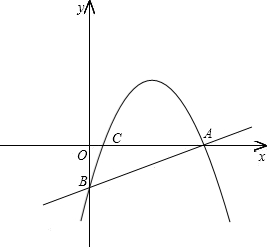
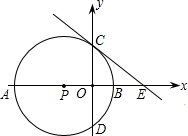 D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E.
D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E.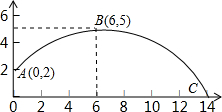 某个二次函数图象的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5).
某个二次函数图象的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5).
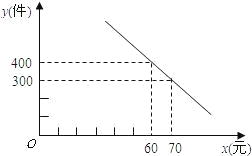 间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?
间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?