题目内容
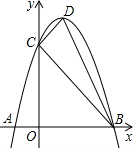
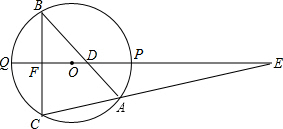
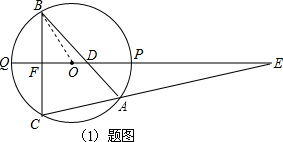
如图,已知△ABC内接于半径为4的☉0,过0作BC的垂线,垂足为F,且交☉0于P、Q两点.OD、OE的长分别是抛物线y=x2+2mx+m2-9与x轴的两个交点的横坐标.
(1)求抛物线的解析式;
(2)是否存在直线l,使它经过抛物线与x轴的交点,并且原点到直线l的距离是2?如果存在,请求出直线l的解析式;如果不存在,请说明理由.
(1)求抛物线的解析式;
(2)是否存在直线l,使它经过抛物线与x轴的交点,并且原点到直线l的距离是2?如果存在,请求出直线l的解析式;如果不存在,请说明理由.

(1)如图,连接BO,∵OQ⊥BC与F,
∴
=
,
∴∠BAC=∠BOQ,
∵∠BOD=180°-∠BOQ,∠EAD=180°-∠BAC,
∴∠BOD=EAD,
又∵∠BDO=∠EDA(对顶角相等),
∴△BOD∽△EAD,
∴
=
,
∴AD•BD=OD•DE,
根据相交弦定理AD•BD=DQ•DP,
∴OD•DE=DQ•DP,
∵圆的半径为4,
∴OD(OE-OD)=(4+OD)(4-OD),
整理得,OD•OE=16,
令y=0,则x2+2mx+m2-9=0,
∵OD、OE是抛物线与x轴的交点的横坐标,
∴OD•OE=m2-9,
∴m2-9=16,
解得m=±5,
∵线段OD、OE的长度都是正数,
∴-
=-
=-m>0,
解得m<0,
∴m=-5,
∴抛物线解析式为y=x2-10x+16;
(2)存在.
理由如下:令y=0,则x2-10x+16=0,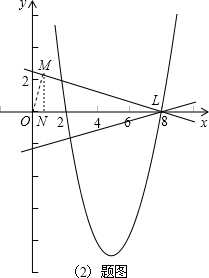
解得x1=2,x2=8,
所以,抛物线与x轴的交点坐标为(2,0),(8,0),
①当直线l经过点(2,0)时,直线l平行于y轴时,原点到直线l的距离为2,
所以,直线l的解析式为x=2;
②当直线l经过点(8,0)时,如图,设点L(8,0),
过点O作OM⊥l与点M,过点M作MN⊥x轴于点N,则OM=2,
∵∠OML=∠MNO=90°,∠MON=∠LOM,
∴△OMN∽△OLM,
∴
=
,
即
=
,
解得ON=
,
在Rt△OMN中,MN=
=
=
,
设直线l的解析式为y=kx+b,
当点M在x轴上方时,点M的坐标为(
,
),
则
,
解得
,
此时直线l的解析式为y=-
x+
,
当点M在x轴下方时,点M的坐标为(
,-
),
则
,
解得
,
此时直线l的解析式为y=
x-
,
综上所述,存在直线l:x=2或y=-
x+
或y=
x-
使原点到l的距离为2.
∴
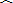 |
| QB |
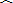 |
| QC |
∴∠BAC=∠BOQ,
∵∠BOD=180°-∠BOQ,∠EAD=180°-∠BAC,
∴∠BOD=EAD,
又∵∠BDO=∠EDA(对顶角相等),
∴△BOD∽△EAD,
∴
| OD |
| AD |
| BD |
| DE |
∴AD•BD=OD•DE,
根据相交弦定理AD•BD=DQ•DP,
∴OD•DE=DQ•DP,
∵圆的半径为4,
∴OD(OE-OD)=(4+OD)(4-OD),
整理得,OD•OE=16,
令y=0,则x2+2mx+m2-9=0,
∵OD、OE是抛物线与x轴的交点的横坐标,
∴OD•OE=m2-9,
∴m2-9=16,
解得m=±5,
∵线段OD、OE的长度都是正数,
∴-
| b |
| 2a |
| 2m |
| 2×1 |
解得m<0,
∴m=-5,
∴抛物线解析式为y=x2-10x+16;
(2)存在.
理由如下:令y=0,则x2-10x+16=0,

解得x1=2,x2=8,
所以,抛物线与x轴的交点坐标为(2,0),(8,0),
①当直线l经过点(2,0)时,直线l平行于y轴时,原点到直线l的距离为2,
所以,直线l的解析式为x=2;
②当直线l经过点(8,0)时,如图,设点L(8,0),
过点O作OM⊥l与点M,过点M作MN⊥x轴于点N,则OM=2,
∵∠OML=∠MNO=90°,∠MON=∠LOM,
∴△OMN∽△OLM,
∴
| OM |
| OL |
| ON |
| OM |
即
| 2 |
| 8 |
| ON |
| 2 |
解得ON=
| 1 |
| 2 |
在Rt△OMN中,MN=
| OM2-ON2 |
22-(
|
| ||
| 2 |
设直线l的解析式为y=kx+b,
当点M在x轴上方时,点M的坐标为(
| 1 |
| 2 |
| ||
| 2 |
则
|
解得
|
此时直线l的解析式为y=-
| ||
| 15 |
8
| ||
| 15 |
当点M在x轴下方时,点M的坐标为(
| 1 |
| 2 |
| ||
| 2 |
则
|
解得
|
此时直线l的解析式为y=
| ||
| 15 |
8
| ||
| 15 |
综上所述,存在直线l:x=2或y=-
| ||
| 15 |
8
| ||
| 15 |
| ||
| 15 |
8
| ||
| 15 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
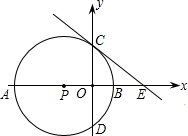 D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E.
D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E.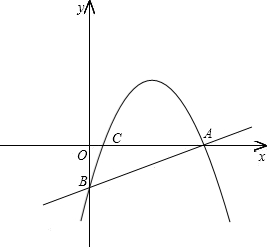
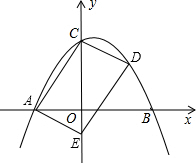
 ,动点Q以每秒2个单位长度的速度沿A→O→D→C→B运动.AO1交于轴于点E,设P、Q运动的时间为t秒.
,动点Q以每秒2个单位长度的速度沿A→O→D→C→B运动.AO1交于轴于点E,设P、Q运动的时间为t秒.