题目内容
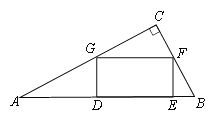
【题目】如图,在Rt△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在边AC、BC上,D、E在边AB上.
(1)求证:△ADG∽△FEB;
(2)若AD=2GD,则△ADG面积与△BEF面积的比为 .
【答案】(1)证明见解析;(2)4.
【解析】
(1)易证∠AGD=∠B,根据∠ADG=∠BEF=90°,即可证明△ADG∽△FEB;
(2)相似三角形的性质解答即可.
(1)证明:∵∠C=90°,
∴∠A+∠B=90°,
∵四边形DEFG是矩形,
∴∠GDE=∠FED=90°,
∴∠GDA+∠FEB=90°,
∴∠A+∠AGD=90°,
∴∠B=∠AGD,
且∠GDA=∠FEB=90°,
∴△ADG∽△FEB.
(2)解:∵△ADG∽△FEB,
∴![]() ,
,
∵AD=2GD,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如下表所示:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当4<x<1时,直接写出y的取值范围.