题目内容
【题目】在平面直角坐标系
中，抛物线
经过点
，
.
（1）求该抛物线的函数表达式及对称轴；
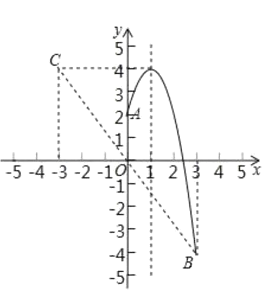
（2）设点
关于原点的对称点为
，点
是抛物线对称轴上一动点，记抛物线在
，之间的部分为图象
（包含，两点），如果直线
与图象有一个公共点，结合函数的图象，直接写出点纵坐标
的取值范围.
【答案】（1）抛物线的表达式为
，抛物线的对称轴为
；（2）
或
.
【解析】
(1)将点A、B代入利用待定系数法解出即可.
(2)由题意确定C坐标,以及二次函数的最小值,确定出D纵坐标的最小值,求直线AC解析式,令x=1求出y的值,由对称性即可得范围.
解：（1）∵点
，
在抛物线
上，
∴
解得
∴抛物线的表达式为.
∴抛物线的对称轴为.
（2）由题意得:C(-3,4),二次函数的最大值为4.
设直线AC:y=kx+b,
将点A和C代入得:
,解得: 
.
∴直线AC的表达式为
.
当x=1时, 
.
由对称性可知,此时与BC交点的纵坐标为: 
.
∴点D纵坐标t的范围为:或.
练习册系列答案
导学教程高中新课标系列答案
相关题目
【题目】某一天，水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克，后再到水果市场去卖，已知猕猴桃和芒果当天的批发价和零售价如表所示：
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
他购进的猕猴桃和芒果各多少千克？
如果猕猴桃和芒果全部卖完，他能赚多少钱？
【题目】一辆汽车油箱中有汽油
.如果不再加油，那么油箱中的油量
（单位：
）随行驶路程
（单位：
）的增加而减少.已知该汽车平均耗油量为
.
（Ⅰ）计算并填写下表：
| 10 | 100 | 300 | … |
| … |
（Ⅱ）写出表示与的函数关系式，并指出自变量的取值范围；
（Ⅲ）若
，
两地的路程约有
，当油箱中油量少于
时，汽车会自动报警，则这辆汽车在由地到
地，再由地返回地的往返途中，汽车是否会报警？请说明理由.
