题目内容
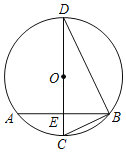
【题目】如图,CD是⊙O的直径,AB是⊙O的弦,CD⊥AB,垂足为E,连接BC、BD.点F为线段CB上一点,连接DF,若CE=2,AB=8,BF=![]() ,则tan∠CDF=__.
,则tan∠CDF=__.
【答案】![]()
【解析】
连接OA,如图,设⊙O的半径为r,则OA=r,OE=r﹣2,利用垂径定理得到AE=BE=![]() AB=4,再利用勾股定理计算出BC=2
AB=4,再利用勾股定理计算出BC=2![]() ,42+(r﹣2)2=r2,解得r=5,则OE=3,接着判断F点为BC的中点,作FH⊥CE于H,则FH=
,42+(r﹣2)2=r2,解得r=5,则OE=3,接着判断F点为BC的中点,作FH⊥CE于H,则FH=![]() BE=2,HE=
BE=2,HE=![]() CE=1,然后利用正切的定义得到tan∠CDF的值.
CE=1,然后利用正切的定义得到tan∠CDF的值.
连接OA,如图,设⊙O的半径为r,则OA=r,OE=r﹣2,
∵CD⊥AB,
∴AE=BE=![]() AB=4,
AB=4,
在Rt△BCE中,BC=![]() =2
=2![]() ,
,
在Rt△OAE中,42+(r﹣2)2=r2,解得r=5,
∴OE=3,
∵BF=![]() ,
,
∴F点为BC的中点,
作FH⊥CE于H,如图,
∴FH为△BCE的中位线,
∴FH=![]() BE=2,HE=
BE=2,HE=![]() CE=1,
CE=1,
在Rt△DHF中,tan∠CDF=![]() =
=![]() =
=![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目