题目内容
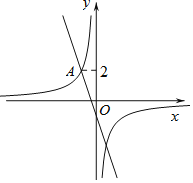
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.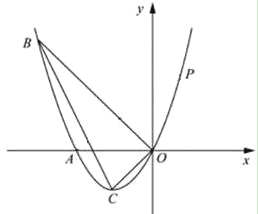
【答案】(1)抛物线的解析式为y=x2+2x;(2)D1(-1,-1),D2(-3,3),D3(1,3);(3)存在,P(![]() ,
,![]() )或(3,15).
)或(3,15).
【解析】
(1)根据抛物线过A(2,0)及原点可设y=a(x-2)x,然后根据抛物线y=a(x-2)x过B(3,3),求出a的值即可;
(2)首先由A的坐标可求出OA的长,再根据四边形AODE是平行四边形,D在对称轴直线x=-1右侧,进而可求出D横坐标为:-1+2=1,代入抛物线解析式即可求出其横坐标;
(3)分△PMA∽△COB和△PMA∽△BOC表示出PM和AM,从而表示出点P的坐标,代入求得的抛物线的解析式即可求得t的值,从而确定点P的坐标.
解:(1)根据抛物线过A(-2,0)及原点,可设y=a(x+2)(x-0),
又∵抛物线y=a(x+2)x过B(-3,3),
∴-3(-3+2)a=3,
∴a=1,
∴抛物线的解析式为y=(x+2)x=x2+2x;
(2)①若OA为对角线,则D点与C点重合,点D的坐标应为D(-1,-1);
②若OA为平行四边形的一边,则DE=OA,∵点E在抛物线的对称轴上,
∴点E横坐标为-1,
∴点D的横坐标为1或-3,代入y=x2+2x得D(1,3)和D(-3,3),
综上点D坐标为(-1,-1),(-3,3),(1,3).
(3)∵点B(-3,3)C(-1,-1),
∴△BOC为直角三角形,∠COB=90°,且OC:OB=1:3,
①如图1,
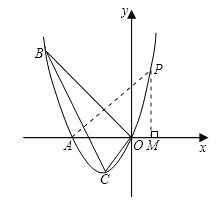
若△PMA∽△COB,设PM=t,则AM=3t,
∴点P(3t-2,t),
代入y=x2+2x得(-2+3t)2+2(-2+3t)=t,
解得t1=0(舍),t2=![]() ,
,
∴P(![]() ,
,![]() );
);
②如图2,
若△PMA∽△BOC,
设PM=3t,则AM=t,点P(t-2,3t),代入y=x2+2x得(-2+t)2+2(-2+t)=3t,
解得t1=0(舍),t2=5,
∴P(3,15)
综上所述,点P的坐标为(![]() ,
,![]() )或(3,15).
)或(3,15).