题目内容
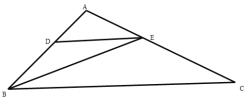
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= ![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.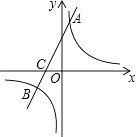
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.
【答案】
(1)解:过点A作AD⊥x轴,垂足为D
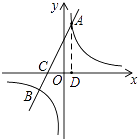
由A(n,6),C(﹣2,0)可得,
OD=n,AD=6,CO=2
∵tan∠ACO=2
∴ ![]() =2,即
=2,即 ![]() =2
=2
∴n=1
∴A(1,6)
将A(1,6)代入反比例函数,得m=1×6=6
∴反比例函数的解析式为 ![]()
将A(1,6),C(﹣2,0)代入一次函数y=kx+b,可得
![]()
解得 ![]()
∴一次函数的解析式为y=2x+4
(2)解:由 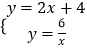 可得,
可得, ![]()
解得x1=1,x2=﹣3
∵当x=﹣3时,y=﹣2
∴点B坐标为(﹣3,﹣2)
【解析】(1)过点A作AD⊥x轴,根据tan∠ACO=2,求出点A的坐标,再根据待定系数法求得一次函数的解析式;(2)把两个函数解析式联立,解方程组求得点B的坐标.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
【题目】某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.
频率分布表
组别 | 分组 | 频数 | 频率 |
1 | 15~25 | 7 | 0.14 |
2 | 25~35 | a | 0.24 |
3 | 35~45 | 20 | 0.40 |
4 | 45~55 | 6 | b |
5 | 55~65 | 5 | 0.10 |
注:这里的15~25表示大于等于15同时小于25.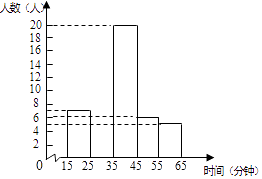
(1)求被调查的学生人数;
(2)直接写出频率分布表中的a和b的值,并补全频数分布直方图;
(3)若该校共有学生500名,则平均每天课外阅读的时间不少于35分钟的学生大约有多少名?