题目内容
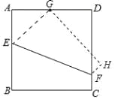
【题目】如图，将边长为4的正方形ABCD沿着折痕EF折叠，使点B落在边AD的中点G处.
(1)求线段BE的长；
(2)连接BF、GF，求证：BF=GF；
(3)求四边形BCFE的面积.
【答案】（1）
；（2）证明见解析；（3）
.
【解析】
（1）由折叠的性质可得
，
，设
，则
，在
中利用勾股定理求出
的值；
（2）根据折叠的性质即可求解；
（3）四边形
是梯形，要求其面积需要得出
的长，可通过求出
的长度，进行求解.
（1）由题意，点
与点
，点
与点
分别关于直线
对称，
，，
设，则，
四边形
是正方形，
，
，
落在边
的中点处，
，
，
解得：
，
.
（2）将边长为
的正方形沿着折痕折叠，使点落在边的中点处，连接BF、GF,在△BFE和△GFE中，BE=GE,∠BEF=∠GEF,EF=EF,∴△BFE≌△GFE
；
（3）
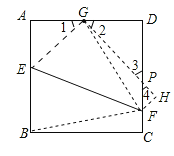
四边形是正方形，
，
，
点
、
分别在
、
边上，
四边形是直角梯形，
，
，
，
，
，
，
，
，
，
在
中， 
，
，
，
，
，
，
，
在
中， 
，
，
.
练习册系列答案
相关题目
