题目内容
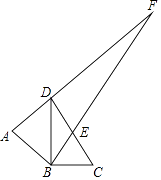
【题目】如图，△ABD是以BD为斜边的等腰直角三角形，△BCD中，∠DBC=90°，∠BCD=60°，DC中点为E，AD与BE的延长线交于点F，则∠AFB的度数为（ ）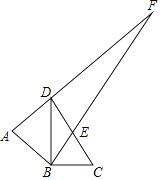
A.30°
B.15°
C.45°
D.25°
【答案】B
【解析】解：∵∠DBC=90°，E为DC中点，
∴BE=CE= 
CD，
∵∠BCD=60°，
∴∠CBE=60°，∴∠DBF=30°，
∵△ABD是等腰直角三角形，
∴∠ABD=45°，
∴∠ABF=75°，
∴∠AFB=180°﹣90°﹣75°=15°，
所以答案是：B．
【考点精析】本题主要考查了等腰直角三角形和直角三角形斜边上的中线的相关知识点，需要掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；直角三角形斜边上的中线等于斜边的一半才能正确解答此题．
练习册系列答案
相关题目
