题目内容
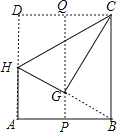
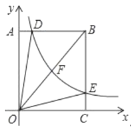
【题目】如图1,点P(m,n)在一次函数y=﹣x的图象上,将点P绕点A(﹣![]() ,﹣
,﹣![]() )逆时针旋转45°,旋转后的对应点为P′.
)逆时针旋转45°,旋转后的对应点为P′.
(1)当m=0时,求点P′的坐标;
(2)试说明:不论m为何值,点P′的纵坐标始终不变;
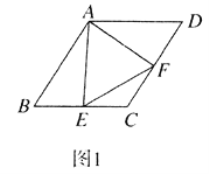
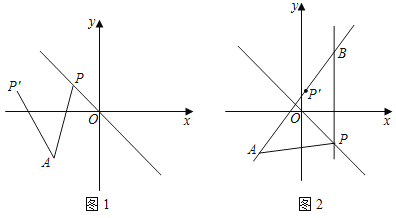
(3)如图2,过点P作x轴的垂线交直线AP′于点B,若直线PB与二次函数y=﹣x2﹣x+2的图象交于点Q,当m>0时,试判断点B是否一定在点Q的上方,请说明理由.
【答案】(1)![]() ;(2)见解析;(3)点 B一定在点Q的上方,见解析
;(2)见解析;(3)点 B一定在点Q的上方,见解析
【解析】
(1)当m=0时,点P(0,0),而点A的坐标为(﹣![]() ,﹣
,﹣![]() ),则点A在直线y=x上且PA=2,进而求解;
),则点A在直线y=x上且PA=2,进而求解;
(2)点A的坐标为(﹣![]() ,﹣
,﹣![]() ),故点A在直线y=x上,则点P′A∥y轴,即可求解;
),故点A在直线y=x上,则点P′A∥y轴,即可求解;
(3)求出直线AB的函数关系式为:y=![]() x+
x+![]() ﹣
﹣![]() ,再求出点P、Q的坐标,即可求解.
,再求出点P、Q的坐标,即可求解.
(1)当m=0时,点P(0,0),
∵点A的坐标为(﹣![]() ,﹣
,﹣![]() ),
),
故点A在直线y=x上且PA=2,
∵点P绕点A(﹣![]() ,﹣
,﹣![]() )逆时针旋转45°,
)逆时针旋转45°,
∴P′A∥y轴,
故![]() ;
;
(2)∵点A的坐标为(﹣![]() ,﹣
,﹣![]() ),
),
故点A在直线y=x上,则点P′A∥y轴,
∵P′A=PA=2,
∴点P 的纵坐标均为![]() ;
;
(3)点 B一定在点Q的上方,理由:
根据条件首先求出P'的坐标![]() ,
,
设直线AB的表达式为:y=kx+b,
将点A、P′的坐标代入上式得: ,解得
,解得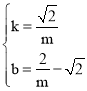 ,
,
从而求出直线AB的函数关系式为:y=![]() x+
x+![]() ﹣
﹣![]() ,
,
当x=m时,y=![]() ,即点B(m,
,即点B(m,![]() ),
),
当x=m时,yQ=﹣m2﹣m+2,即点Q(m,﹣m2﹣m+2),
∴yB﹣yQ=![]() ﹣(﹣m2﹣m+2)=m2+
﹣(﹣m2﹣m+2)=m2+![]() ,
,
∵m>0
∴![]()
∴yB>yQ
∴点 B一定在点Q的上方.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】甲、乙两校各选派10名学生参加“美丽泰州乡土风情知识”大赛预赛.各参赛选手的成绩如下:
甲校:93,98,89,93, 95,96, 93,96,98, 99;
乙校:93,94,88,91,92,93,100, 98,98,93.
通过整理,得到数据分析表如下:
学校 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
甲校 | 99 | a | 95.5 | 93 | 8.4 |
乙校 | 100 | 94 | b | 93 | c |
(1)填空:a = ,b = ;
(2)求出表中c的值,你认为哪所学校代表队成绩好?请写出两条你认为该队成绩好的理由.