题目内容
【题目】下图为某小区的两幢1O层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.现需了解在某一时段内,甲楼对乙楼的采光的影响情况.假设某一时刻甲楼楼顶B落在乙楼的影子长EC=h,太阳光线与水平线的夹角为α.
(1)用含α的式子表示h;
(2)当α=30°时,甲楼楼顶B的影子落在乙楼的第几层?从此时算起,若α每小时增加10°,几小时后,甲楼的影子刚好不影响乙楼采光.
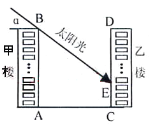
【答案】(1)30-30tanα(2)甲楼顶B的影子落在第五层;应在1个半小时后,甲楼的影子刚好不影响乙楼的采光
【解析】
(1)过E作EF⊥AB,垂足为F,在直角三角形BFE中,用锐角三角函数表示出h即可;
(2)令α=30°求得h的近似值后即可判断影子落在第几层.结合题中数据可知不影响采光时α为45°,再根据每小时增加10°,即可得解.
⑴过E作EF⊥AB,垂足为F,则∠BEF=α
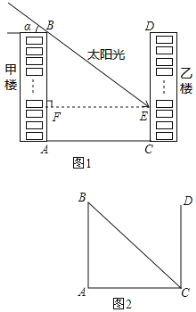
在Rt△BFE中,FE=AC=30,AB=10×3=30
∴BF=AB-EC=30-h
∵tanα=![]() ,∴BF=EF×tanα
,∴BF=EF×tanα
即30-h=30×tanα
h=30-30tanα
⑵、当α=300时,h=30-30tan300≈12.68
∴甲楼顶B的影子落在第五层
不影响乙楼的采光时,AB的影子顶部应刚好落在C处,
此时,AB=30,AC=30,
∴∠BCA=450,
则∠α=450,
∵角α每小时增加10度,
∴应在1个半小时后,甲楼的影子刚好不影响乙楼的采光.

练习册系列答案
相关题目