题目内容
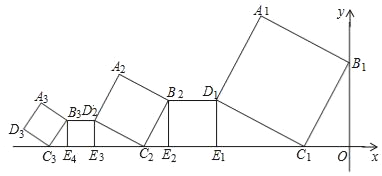
【题目】一组正方形按如图所示的方式放置，其中顶点B1在y轴上，顶点C1，E1，E2，C2，E3，E4，C3……在x轴上，已知正方形A1B1C1D1的顶点C1的坐标是（﹣
，0），∠B1C1O=60°，B1C1∥B2C2∥B3C3……则正方形A2018B2018C2018D2018的顶点D2018纵坐标是_____．
【答案】
×（
）2017
【解析】
利用正方形的性质结合锐角三角函数关系得出正方形的边长，进而得出变化规律即可得出答案.
∵∠B1C1O=60°，C1O=，
∴B1C1=1，∠D1C1E1=30°，
∵sin∠D1C1E1=
，
∴D1E1=，
∵B1C1∥B2C2∥B3C3∥…
∴60°=∠B1C1O=∠B2C2O=∠B3C3O=…
∴B2C2=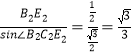
，B3C3=
.
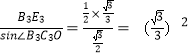故正方形AnBnCnDn的边长=（）n-1．
∴B2018C2018=（）2017．
∴D2018E2018=×（）2017，
∴D的纵坐标为×（）2017，
故答案为×（）2017.
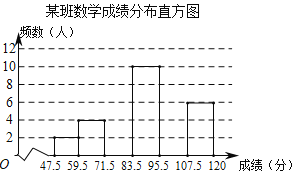
【题目】某市为了解九年级学生数学模拟考试成绩情况，随机抽取部分学生的成绩进行分析，制成频数分布表如下（成绩得分均为整数）：
组别 | 成绩分组 | 频数 | 频率 |
1 | 47.5～59.5 | 2 | 0.05 |
2 | 59.5～71.5 | 4 | 0.10 |
3 | 71.5～83.5 | a | 0.2 |
4 | 83.5～95.5 | 10 | 0.25 |
5 | 95.5～107.5 | b | c |
6 | 107.5～120 | 6 | 0.15 |
合计 | d | 1.00 |
根据表中提供的信息解答下列问题：
（1）频数分布表中的a＝ ，b＝ ，c＝ ，d＝ ；
（2）补充完整频数分布直方图．
（3）已知全市九年级共有3500名学生参加考试，成绩96分及以上为优秀，估计全市九年级学生数学模拟考试成绩为优秀的学生人数是多少？
【题目】“古圣先贤孝为宗，万善之门孝为基，礼敬尊亲如活佛，成就生命大意义，父母恩德重如山，知恩报恩不忘本，做人饮水要思源，才不愧对父母恩…”.某实验中学为加强对学生的感恩教育，教学生唱《跪羊图》，并对学生的学习成果进行随机抽查，现对部分学生的成绩（x为整数，满分100分）进行了统计，绘制了如下尚不完整的统计图表.
组别 | 成绩分组 （单位：分） | 频数 | 频率 |
A |
| 40 | 0.1 |
B |
| 60 | c |
C |
| a | 0.2 |
D |
| 160 | 0.4 |
E |
| 60 | 0.15 |
合计 | b | 1 |
调查结果扇形统计图
根据以上信息解答下列问题：/p>
（1）统计表中
________，
________，
________；
（2）求扇形统计图中D组所在扇形的圆心角的度数；
（3）若参加《跪羊图》演唱的同学共有2000人，请估计成绩在90分及以上的学生有多少人？