ЬтФПФкШн
ЁОЬтФПЁПСЊЯыЮвУЧдјОбЇЯАЙ§ЕФШ§НЧаЮЭтаФЕФИХФюЃЌЮвУЧПЩв§ШызМЭтаФЕФЖЈвхЃКЕНШ§НЧаЮЕФСНИіЖЅЕуОрРыЯрЕШЕФЕуЃЌНазіДЫШ§НЧаЮЕФзМЭтаФЃЎЧыЛиД№ЯТУцЕФШ§ИіЮЪЬтЃК

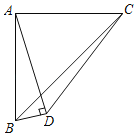
ЃЈ1ЃЉШчЭМ1ЃЌШєPBЃНPCЃЌдђЕуPЮЊЁїABCЕФзМЭтаФЃЌЖјЧвЮвУЧжЊЕРТњзуДЫЬѕМўЕФзМЭтаФгаЮоЪ§ЖрИіЃЌФуФмЗёгУГпЙцзїГіСэЭтвЛИізМЭтаФQФиЃПЧыГЂЪдЭъГЩЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌвбжЊЁїABCЮЊжБНЧШ§НЧаЮЃЌаББпBCЃН5ЃЌABЃН3ЃЌзМЭтаФPдкACБпЩЯЃЌЪдЬНОПPAЕФГЄЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕуBМШЪЧЁїEDCгжЪЧЁїADCЕФзМЭтаФЃЌBDЃНBAЃНBCЃН2ADЃЌBDЁЮACЃЌCDЃН![]() ЃЌЧѓADЕФжЕЃЎ
ЃЌЧѓADЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉФмгУГпЙцзїГіСэЭтвЛИізМЭтаФQЃЌШчЭМ1ЫљЪОЃКЕуQЮЊЁїABCЕФзМЭтаФЃЛЃЈ2ЃЉзМЭтаФPдкACБпЩЯЃЌPAЕФГЄЮЊ![]() Лђ2ЃЛЃЈ3ЃЉADЃН
Лђ2ЃЛЃЈ3ЃЉADЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉзїABЕФДЙжБЦНЗжЯпMNЃЌдкMNЩЯШЁЕуQМДПЩЃЛ
ЃЈ2ЃЉСЌНгBPЃЌгЩЙДЙЩЖЈРэЕУГіAC=4ЃЌЗжШ§жжЧщПіЬжТлЃЌгЩжБНЧШ§НЧаЮЕФаджЪМДПЩЕУГіД№АИЃЛ
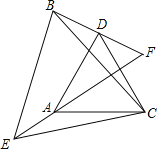
ЃЈ3ЃЉгЩBD=BA=BCЃЌЕУГіЁЯBAC=ЁЯBCAЃЌЕуDЁЂAЁЂCдквдBЮЊдВаФЃЌABГЄЮЊАыОЖЕФдВЩЯЃЌгЩдВжмНЧЖЈРэЕУГіЁЯABD=2ЁЯACDЃЌзїBEЁЭCDгкEЃЌBFЁЭADгкFЃЌгЩДЙОЖЖЈРэЕУГіDE=CE![]() CD
CD![]() ЃЌDF=AF
ЃЌDF=AF![]() ADЃЌЁЯABD=2ЁЯDBFЃЌЁЯBEC=ЁЯDFB=90ЁуЃЌжЄУїЁїBDFЁеЁїCBEЃЌЕУГіDF=BEЃЌЩшDF=xЃЌдђBE=xЃЌAD=2xЃЌBD=2AD=4xЃЎдкRtЁїBDEжаЃЌгЩЙДЙЩЖЈРэЕУГіЗНГЬЃЌНтЗНГЬМДПЩЃЎ
ADЃЌЁЯABD=2ЁЯDBFЃЌЁЯBEC=ЁЯDFB=90ЁуЃЌжЄУїЁїBDFЁеЁїCBEЃЌЕУГіDF=BEЃЌЩшDF=xЃЌдђBE=xЃЌAD=2xЃЌBD=2AD=4xЃЎдкRtЁїBDEжаЃЌгЩЙДЙЩЖЈРэЕУГіЗНГЬЃЌНтЗНГЬМДПЩЃЎ
ЃЈ1ЃЉФмгУГпЙцзїГіСэЭтвЛИізМЭтаФQЃЌ
зїABЕФДЙжБЦНЗжЯпMNЃЌдкMNЩЯШЁЕуQЃЌШчЭМ1ЫљЪОЃК
дђQA=QBЃЌЕуQЮЊЁїABCЕФзМЭтаФЃЛ
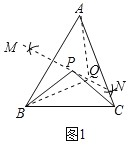
ЃЈ2ЃЉСЌНгBPЃЌШчЭМ2ЫљЪОЃК
ЁпЁїABCЮЊжБНЧШ§НЧаЮЃЌаББпBC=5ЃЌAB=3ЃЌ
ЁрAC![]() 4ЃЎ
4ЃЎ
ЁпзМЭтаФPдкACБпЩЯЃЌ
ЂйЕБPB=PCЪБЃЌ
ЩшPB=xЃЌдђPC=xЃЌPA=4ЉxЃЌ
дкRtЁїABPжаЃЌгЩЙДЙЩЖЈРэЕУЃК32+ЃЈ4ЉxЃЉ2=x2ЃЌ
НтЕУЃКx![]() ЃЌ
ЃЌ
ЁрPA=4![]() ЃЛ
ЃЛ
ЂкЕБPA=PCЪБЃЌPA![]() AC=2ЃЛ
AC=2ЃЛ
ЂлЕБPA=PBЪБЃЎ
ЁпЁїABCЪЧжБНЧШ§НЧаЮЃЌЁрДЫЧщПіВЛДцдкЃЎ
злЩЯЫљЪіЃКзМЭтаФPдкACБпЩЯЃЌPAЕФГЄЮЊ![]() Лђ2ЃЛ
Лђ2ЃЛ
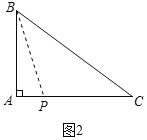
ЃЈ3ЃЉЁпBD=BA=BCЃЌЁрЁЯBAC=ЁЯBCAЃЌЕуDЁЂAЁЂCдквдBЮЊдВаФЃЌABГЄЮЊАыОЖЕФдВЩЯЃЌШчЭМ3ЫљЪОЃЌдђЁЯABD=2ЁЯACDЃЎ
зїBEЁЭCDгкEЃЌBFЁЭADгкFЃЌ
дђDE=CE![]() CD
CD![]() ЃЌDF=AF
ЃЌDF=AF![]() ADЃЌ
ADЃЌ
ЁЯABD=2ЁЯDBFЃЌЁЯBEC=ЁЯDFB=90ЁуЃЎ
ЁпBDЁЮACЃЌ
ЁрЁЯABD=ЁЯBAC=ЁЯBCA=2ЁЯACD=2ЁЯDBF=2ЁЯBCEЃЌ
ЁрЁЯDBF=ЁЯBCEЃЎ
дкЁїBDFКЭЁїCBEжаЃЌЁп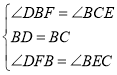 ЃЌ
ЃЌ
ЁрЁїBDFЁеЁїCBEЃЈASAЃЉЃЌЁрDF=BEЃЎ
ЩшDF=xЃЌдђBE=xЃЌAD=2xЃЌBD=2AD=4xЃЌ
дкRtЁїBDEжаЃЌгЩЙДЙЩЖЈРэЕУЃКx2+ЃЈ![]() ЃЉ2=ЃЈ4xЃЉ2ЃЌ
ЃЉ2=ЃЈ4xЃЉ2ЃЌ
НтЕУЃКx![]() ЃЌЁрAD=2x
ЃЌЁрAD=2x![]() ЃЎ
ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ