ΧβΡΩΡΎ»ί
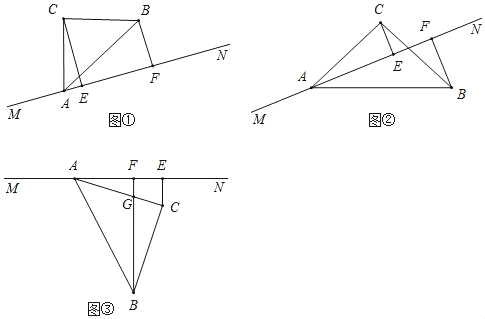
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΒ»―ϋ÷±Ϋ«ΓςABC÷–Θ§ΓœC «÷±Ϋ«Θ§ΒψA‘Ύ÷±œΏMN…œΘ§ΙΐΒψCΉςCEΓΆMN”ΎΒψEΘ§ΙΐΒψBΉςBFΓΆMN”ΎΒψFΘ°
Θ®1Θ©»γΆΦ1Θ§Β±CΘ§BΝΫΒψΨυ‘Ύ÷±œΏMNΒΡ…œΖΫ ±Θ§
ΔΌ÷±Ϋ”–¥≥ωœΏΕΈAEΘ§BF”κCEΒΡ ΐΝΩΙΊœΒΘ°
ΔΎ≤¬≤βœΏΕΈAFΘ§BF”κCEΒΡ ΐΝΩΙΊœΒΘ§≤Μ±Ί–¥≥ω÷ΛΟςΙΐ≥ΧΘ°
Θ®2Θ©ΫΪΒ»―ϋ÷±Ϋ«ΓςABC»ΤΉ≈ΒψAΥ≥ ±’κ–ΐΉΣ÷ΝΆΦ2ΈΜ÷Ο ±Θ§œΏΕΈAFΘ§BF”κCE”÷”–‘θ―υΒΡ ΐΝΩΙΊœΒΘ§«κ–¥≥ωΡψΒΡ≤¬œκΘ§≤Δ–¥≥ω÷ΛΟςΙΐ≥ΧΘ°
Θ®3Θ©ΫΪΒ»―ϋ÷±Ϋ«ΓςABC»ΤΉ≈ΒψAΦΧ–χ–ΐΉΣ÷ΝΆΦ3ΈΜ÷Ο ±Θ§BF”κACΫΜ”ΎΒψGΘ§»τAF=3Θ§BF=7Θ§÷±Ϋ”–¥≥ωFGΒΡ≥ΛΕ»Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌAE+BF =ECΘΜΔΎAF+BF=2CEΘΜΘ®2Θ©AF©¹BF=2CEΘ§÷ΛΟςΦϊΫβΈωΘΜΘ®3Θ©FG=![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΔΌ÷Μ“Σ÷ΛΟςΓςACEΓ’ΓςBCDΘ®AASΘ©Θ§ΆΤ≥ωAE=BDΘ§CE=CDΘ§ΆΤ≥ωΥΡ±Ώ–ΈCEFDΈΣ’ΐΖΫ–ΈΘ§Φ¥Ω…ΫβΨωΈ ΧβΘΜ
ΔΎάϊ”ΟΔΌ÷–Ϋα¬έΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®2Θ© Ήœ»÷ΛΟςBF-AF=2CEΘ°”…AF=3Θ§BF=7Θ§ΆΤ≥ωCE=EF=2Θ§AE=AF+EF=5Θ§”…FGΓΈECΘ§Ω…÷Σ![]() Θ§”…¥ΥΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ§”…¥ΥΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®1Θ©÷ΛΟςΘΚΔΌ»γΆΦ1Θ§ΙΐΒψCΉωCDΓΆBFΘ§ΫΜFBΒΡ―”≥ΛœΏ”ΎΒψDΘ§
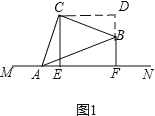
ÿCEâMNȧCDâBFȧ
ΓύΓœCEA=ΓœD=90ΓψΘ§
ÿCEâMNȧCDâBFȧBFâMNȧ
ΓύΥΡ±Ώ–ΈCEFDΈΣΨΊ–ΈΘ§
ΓύΓœECD=90ΓψΘ§
”÷ΓΏΓœACB=90ΓψΘ§
ΓύΓœACB-ΓœECB=ΓœECD-ΓœECBΘ§
Φ¥ΓœACE=ΓœBCDΘ§
”÷ΓΏΓςABCΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύAC=BCΘ§
‘ΎΓςACEΚΆΓςBCD÷–Θ§
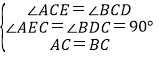 Θ§
Θ§
ΓύΓςACEΓ’ΓςBCDΘ®AASΘ©Θ§
ΓύAE=BDΘ§CE=CDΘ§
”÷ΓΏΥΡ±Ώ–ΈCEFDΈΣΨΊ–ΈΘ§
ΓύΥΡ±Ώ–ΈCEFDΈΣ’ΐΖΫ–ΈΘ§
ΓύCE=EF=DF=CDΘ§
ΓύAE+BF=DB+BF=DF=ECΘ°
ΔΎ”…ΔΌΩ…÷ΣΘΚAF+BF=AE+EF+BF
=BD+EF+BF
=DF+EF
=2CEȧ
Θ®2Θ©AF-BF=2CE
ΆΦ2÷–Θ§ΙΐΒψCΉςCGΓΆBFΘ§ΫΜBF―”≥ΛœΏ”ΎΒψGΘ§
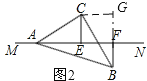
ΓΏAC=BC
Ω…ΒΟΓœAEC=ΓœCGBΘ§
ΓœACE=ΓœBCGΘ§
‘ΎΓςCBGΚΆΓςCAE÷–Θ§
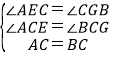 Θ§
Θ§
ΓύΓςCBGΓ’ΓςCAEΘ®AASΘ©Θ§
ΓύAE=BGΘ§
ÿAF=AE+EFȧ
ΓύAF=BG+CE=BF+FG+CE=2CE+BFΘ§
ΓύAF-BF=2CEΘΜ
Θ®3Θ©»γΆΦ3Θ§ΙΐΒψCΉωCDΓΆBFΘ§ΫΜFBΒΡ”ΎΒψDΘ§
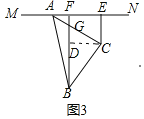
ΓΏAC=BC
Ω…ΒΟΓœAEC=ΓœCDBΘ§
ΓœACE=ΓœBCDΘ§
‘ΎΓςCBDΚΆΓςCAE÷–Θ§
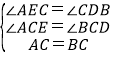 Θ§
Θ§
ΓύΓςCBDΓ’ΓςCAEΘ®AASΘ©Θ§
ΓύAE=BDΘ§
ÿAF=AE-EFȧ
ΓύAF=BD-CE=BF-FD-CE=BF-2CEΘ§
ΓύBF-AF=2CEΘ°
ΓΏAF=3Θ§BF=7Θ§
ΓύCE=EF=2Θ§AE=AF+EF=5Θ§
ÿFGøECȧ
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύFG=![]() Θ°
Θ°