题目内容
【题目】矩形ABCD中,AB=8,AD=6,E为BC边上一点,将△ABE沿着AE翻折,点B落在点F处,当△EFC为直角三角形时BE=_____.
【答案】3或6
【解析】
分当点F落在矩形内部时和当点F落在AD边上时两种情况求BE得长即可.
当△CEF为直角三角形时,有两种情况:

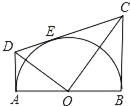
当点F落在矩形内部时,如图1所示.
连结AC,
在Rt△ABC中,AB=6,BC=8,
∴AC=![]()
![]() =10,
=10,
∵∠B沿AE折叠,使点B落在点F处,
∴∠AFE=∠B=90°,
当△CEF为直角三角形时,只能得到∠EFC=90°,
∴点A、F、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点F处,如图,
∴EB=EF,AB=AF=6,
∴CF=10﹣6=4,
设BE=x,则EF=x,CE=8﹣x,
在Rt△CEF中,
∵EF2+CF2=CE2,
∴x2+42=(8﹣x)2,
解得x=3,
∴BE=3;
②当点F落在AD边上时,如图2所示.
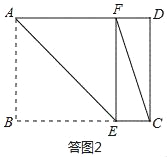
此时ABEF为正方形,
∴BE=AB=6.
综上所述,BE的长为3或6.
故答案为:3或6.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目