题目内容
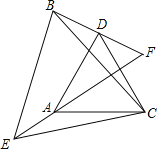
【题目】如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为![]() ,AC=2+2
,AC=2+2![]() ,则△CEF的面积为( )
,则△CEF的面积为( )

A. ![]() B. 2
B. 2![]() C. 2+
C. 2+![]() D. 2
D. 2![]()
【答案】B
【解析】
要求△CEF的面积,关键是求出CE和CF的乘积,根据题目中条件可以证明△EDC≌△FDB,得到CE和BF的关系,再根据勾股定理和⊙O的半径为![]() ,AC=2+2
,AC=2+2![]() ,可以求得CE和CF的乘积,本题得以解决.
,可以求得CE和CF的乘积,本题得以解决.
连接CD、ED、DF、EF,如图所示.
∵AC⊥BC,AC=BC,点D是AB中点,∴CD=DA=DB,∠CDB=90°,∠ECD=∠FBD=45°.
又∵EF是⊙O的直径,∴∠EDF=90°,∴∠EDC+∠CDF=∠CDF+∠FDB=90°,∴∠EDC=∠FDB.
在△EDC和△FDB中,∵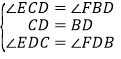 ,∴△EDC≌△FDB(ASA),∴CE=BF.
,∴△EDC≌△FDB(ASA),∴CE=BF.
又∵AC=BC,AC=2+2![]() ,∴BC=2+2
,∴BC=2+2![]() ,即BF+FC=2+2
,即BF+FC=2+2![]() ,∴CF+CE=2+2
,∴CF+CE=2+2![]() .
.
又∵∠ECF=90°,⊙O的半径为![]() ,∴CE2+CF2=EF2,EF=2
,∴CE2+CF2=EF2,EF=2![]() ,解得:CECF=4
,解得:CECF=4![]() ,∴△CEF的面积为:
,∴△CEF的面积为:![]() .
.
故选B.

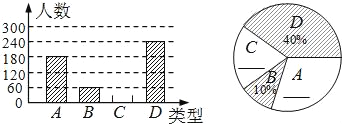
【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |

(1)请直接写出![]() ,
,![]() ,第3组人数在扇形统计图中所对应的圆心角是 度.
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?