题目内容
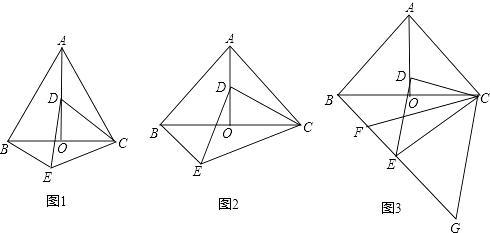
【题目】如图,已知△ABC中,AB=AC=5,BC=6,点O是边BC上的动点,以点O为圆心,OB为半径作圆O,交AB边于点D,过点D作∠ODP=∠B,交边AC于点P,交圆O与点E.设OB=x. 
(1)当点P与点C重合时,求PD的长;
(2)设AP﹣EP=y,求y关于x的解析式及定义域;
(3)联结OP,当OP⊥OD时,试判断以点P为圆心,PC为半径的圆P与圆O的位置关系.
【答案】
(1)解:如图1中,作AH⊥BC于H,CG⊥AB于G,

∵AB=AC=5,AH⊥BC,
∴BH=CH=3,AH=4,
∵ ![]() BCAH=
BCAH= ![]() ABCG,
ABCG,
∴CG= ![]() ,AG=
,AG= ![]() =
= ![]() ,
,
∴cos∠B= ![]() ,cos∠BAC=
,cos∠BAC= ![]() ,
,
如图2中,当点P与C重合时,

∵OB=OD,
∴∠B=∠ODB=∠ACB,
∵∠ADO=∠B+∠BOD=∠CDO+∠ADP,∠ODP=∠B,
∴∠ADP=∠BOD=∠BAC,
∴PA=PD=5;
(2)解:如图2中,作CG⊥AB于G,OH⊥BD于H.

∵AD=2AG= ![]() ,
,
∵BD=2BH=2OBcos∠B= ![]() x,
x,
∴ ![]() x+
x+ ![]() =5,
=5,
∴x= ![]() ,
,
如图3中,当P、E重合时,作EG⊥AD于G.

根据对称性可知,B、E关于直线OD对称,
∴DB=DE=AE= ![]() x,
x,
∵cos∠A= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得x= ![]() ,
,
当点D与A重合时 ![]() x=5,
x=5,
∴x= ![]() ,
,
当 ![]() ≤x≤
≤x≤ ![]() 时,如图4中,
时,如图4中,

∵y=PA﹣PE=PD﹣PE=DE=BD= ![]() x,
x,
∴y= ![]() x,
x,
当 ![]() <x<
<x< ![]() 时,如图5中,作PG⊥AB于G.
时,如图5中,作PG⊥AB于G.

∵BD=DE= ![]() x,DG=AG=
x,DG=AG= ![]() (5﹣
(5﹣ ![]() x),
x),
∴AP=AG÷cos∠A= ![]() (5﹣
(5﹣ ![]() x),
x),
∴y=AP﹣EP= ![]() (5﹣
(5﹣ ![]() x)﹣[
x)﹣[ ![]() x﹣
x﹣ ![]() (5﹣
(5﹣ ![]() x)]=﹣
x)]=﹣ ![]() x+
x+ ![]() ,
,
综上所述,y=  .
.
(3)解:如图6中,连接OP.

连接OP,∵OP⊥AC,
∴cos∠C=cos∠B= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴x= ![]() ,PC=
,PC= ![]() ,OP=
,OP= ![]() ,
,
∵ ![]() <
< ![]() +
+ ![]() ,
,
∴以点P为圆心,PC为半径的圆P与圆O的位置关系是相交.
【解析】(1)如图1中,首先求出cos∠B,cos∠A,如图2中,当点P与C重合时,只要证明PA=PD即可;(2)如图2中,作CG⊥AB于G,OH⊥BD于H.分两种情形①当 ![]() ≤x≤
≤x≤ ![]() 时,如图4中.②当
时,如图4中.②当 ![]() <x<
<x< ![]() 时,如图5中,作PG⊥AB于G.(3)如图6中,连接OP.根据cos∠C=cos∠B=
时,如图5中,作PG⊥AB于G.(3)如图6中,连接OP.根据cos∠C=cos∠B= ![]() =
= ![]() ,列出方程,求出两圆的半径,圆心距即可判断.
,列出方程,求出两圆的半径,圆心距即可判断.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 3 | … |
y | … | ﹣3 | 1 | 3 | 1 | … |
则下列判断正确的是( )
A.抛物线开口向上
B.抛物线与y轴交于负半轴
C.当x=4时,y>0
D.方程ax2+bx+c=0的正根在3与4之间