题目内容
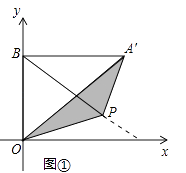
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线y= ![]() x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
(1)求抛物线的解析式;
(2)证明:圆C与x轴相切;
(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求BE:MF的值.
【答案】
(1)
解:∵已知抛物线y=ax2+bx+c(a≠0)的图象的顶点坐标是(2,1),
∴可设抛物线解析式为y=a(x﹣2)2+1,
∵抛物线经过点(4,2),
∴2=a(4﹣2)2+1,解得a= ![]() ,
,
∴抛物线解析式为y= ![]() (x﹣2)2+1=
(x﹣2)2+1= ![]() x2﹣x+2;
x2﹣x+2;
(2)
解:联立直线和抛物线解析式可得 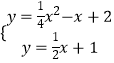 ,解得
,解得 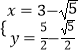 或
或 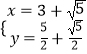 ,
,
∴B(3﹣ ![]() ,
, ![]() ﹣
﹣ ![]() ),D(3+
),D(3+ ![]() ,
, ![]() +
+ ![]() ),
),
∵C为BD的中点,
∴点C的纵坐标为 ![]() =
= ![]() ,
,
∵BD= ![]() =5,
=5,
∴圆的半径为 ![]() ,
,
∴点C到x轴的距离等于圆的半径,
∴圆C与x轴相切;
(3)
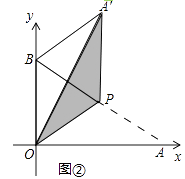
解:如图,过点C作CH⊥m,垂足为H,连接CM,

由(2)可知CM= ![]() ,CH=
,CH= ![]() ﹣1=
﹣1= ![]() ,
,
在Rt△CMH中,由勾股定理可求得MH=2,
∵HF= ![]() =
= ![]() ,
,
∴MF=HF﹣MH= ![]() ﹣2,
﹣2,
∵BE= ![]() ﹣
﹣ ![]() ﹣1=
﹣1= ![]() ﹣
﹣ ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() .
.
【解析】(1)可设抛物线的顶点式,再结合抛物线过点(4,2),可求得抛物线的解析式;(2)联立直线和抛物线解析式可求得B、D两点的坐标,则可求得C点坐标和线段BD的长,可求得圆的半径,可证得结论;(3)过点C作CH⊥m于点H,连接CM,可求得MH,利用(2)中所求B、D的坐标可求得FH,则可求得MF和BE的长,可求得其比值.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.