Question

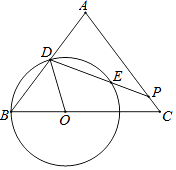
【题目】如图，△ABC中，AB=AC，AO是角平分线，D为AO上一点，作△CDE，使DE=DC，∠EDC=∠BAC，连接BE．

（1）若∠BAC=60°，求证：△ACD≌△BCE；
（2）若∠BAC=90°，AD=DO，求 的值；
（3）若∠BAC=90°，F为BE中点，G为 BE延长线上一点，CF=CG，AD=nDO，直接写出 的值．

Answer 1

【答案】
（1）

证明：如图1中，

∵△ABC和△CDE为等边三角形，

∴AC=BC，CD=CE．∠ACB=∠DCE=60°，

∴∠ACB﹣∠DCO=∠DCE﹣∠DCO，

∴∠ACD=∠BCE，

在△ACD和△BCE中，

，

∴△ACD≌△BCE（SAS）

（2）

如图2中，

∵AB=AC，OA平分∠BAC，

∴AO⊥BC，OB=OC，

∵∠BAC=∠EDC=90°，AB=AC，DE=DC，

∴∠ACB=∠DCE=45°，BC= AC，EC= CD，

∴ = ，∠ACD=∠BCE，

∴△ACD∽△BCE，

∴ = = ，

∵OA=OB=OC，AD=OD，

∴AD= BC，

∴ = ，

∴ =

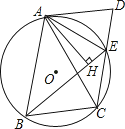
（3）

如图3中，作CH⊥BG于H．

由（2）可知△ACD∽△BCE，

∴BE：AD= ，∠CAD=∠CBE=45°，设OD=k，则AD=nk，BE= nk，AO=（n+1）k，

∵∠ABC=∠HBC=45°，∠BAC=∠BHC，BC=BC，

∴△ABC≌△HBC，

∴BH=CH=AB=AC= （n+1）k，BF= nk，

FH=HG= （n+1）k﹣ nk，

∴ = =

【解析】（1）只要证明∠ACD=∠BCE，即可根据SAS证得△ACD≌△BCE；（2）首先证明△ACD∽△BCE，得 = = ，再根据AD= BC即可解决问题．（3）如图3中，作CH⊥BG于H．设OD=k，则AD=nk，BE= nk，AO=（n+1）k，首先证明△ABC≌△HBC，得BH=CH=AB=AC= （n+1）k，BF= nk，求出BG即可解决问题．
【考点精析】本题主要考查了相似三角形的应用的相关知识点，需要掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解才能正确解答此题．