题目内容
已知点A(1，2)和B(－2，5)，试求出两个二次函数，使它们的图象都经过A、B两点．
y＝x2＋1 y＝
x2＋
x
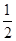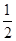x2＋x解：法一 设抛物线y＝ax2＋bx＋c经过点A(1，2)，B(－2，5)，
则①－②得3b－3a＝－3，即a＝b＋1.
设a＝2，则b＝1，将a＝2，b＝1代入①，得c＝－1，
故所求的二次函数为y＝2x2＋x－1.
又设a＝1，则b＝0，将a＝1，b＝0代入①，得c＝1，
故所求的另一个二次函数为.
法二 因为不在同一条直线上的三点确定一条抛物线，因此要确定一条抛物线，可以另外再取一点，不妨取C(0，0)，
则
∴
解得
故所求的二次函数为y＝
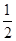x2＋x，用同样的方法可以求出另一个二次函数．
练习册系列答案
53随堂测系列答案
相关题目
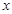轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线
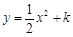与扇形OAB的边界总有两个公共点，则实数
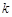的取值范围是 .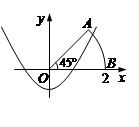
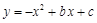经过A（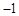
，0）、B（5，0）两点，顶点为P．
，
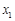）和点D（
，
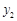）在该抛物线上，则当
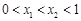时，
的顶点坐标是 .
